A spring is attached to a wooden cubical block of edge 5cm and placed in a water conatiner as shown in figure. Calculate the maximum weight to be placed on the block so that it is just immersed in water completely. Density of wood =700kg/m3, spring constant of spring =70N/m,g=10m/s2. Assume that initially spring is in its normal length. 
Edge of block =5 cm
Density of wood pw=700kg/m3
Speicfic gravity of wood =0.7
Height of block inside of water =5×0.7=3.5cm
Height of block outside water =5−3.5=1.5cm
W=Maximum weight to be put on the block so that it is just immersed.
V=Volume of displaced water
=Volume of block
=5×5×5
=125cm3
=125×10−6m3
Upward buoyant force =Vpg
=125×10−6×1000×10
=1.25N
Here, p=density of water =1000kg/m3
When weight is put on the block, the spring will be compressed by 1.5 cm
To maintain equilibrium, spring will exert an upward force.
Spring force =kx
k=force constant =70 N/m
x=1.5cm=1.5×10−2m
Spring force =70×1.5×10−2N
=1.05 N
Spring force and buoyant force are in upward direction.
Weight of block and additional weight kept on the block act in downward direction.
Total weight of block =W+w=Vpwg+w
=125×10−6×700×10+w
=0.87N+w
1.05+1.25N=0.87+w
w=1.43N
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT (Textbook Exercises)
Explore 20 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT (Additional Exercises)
Explore 11 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Conceptual Questions
Explore 29 Videos
- MATHEMATICAL TOOLSBook:MODERN PUBLICATIONChapter:MATHEMATICAL TOOLSExercise:PRACTICE PROBLEMS (10)
Explore 12 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
Similar Questions
A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,
,
View SolutionA cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,
,
View Solution
Knowledge Check
Two spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
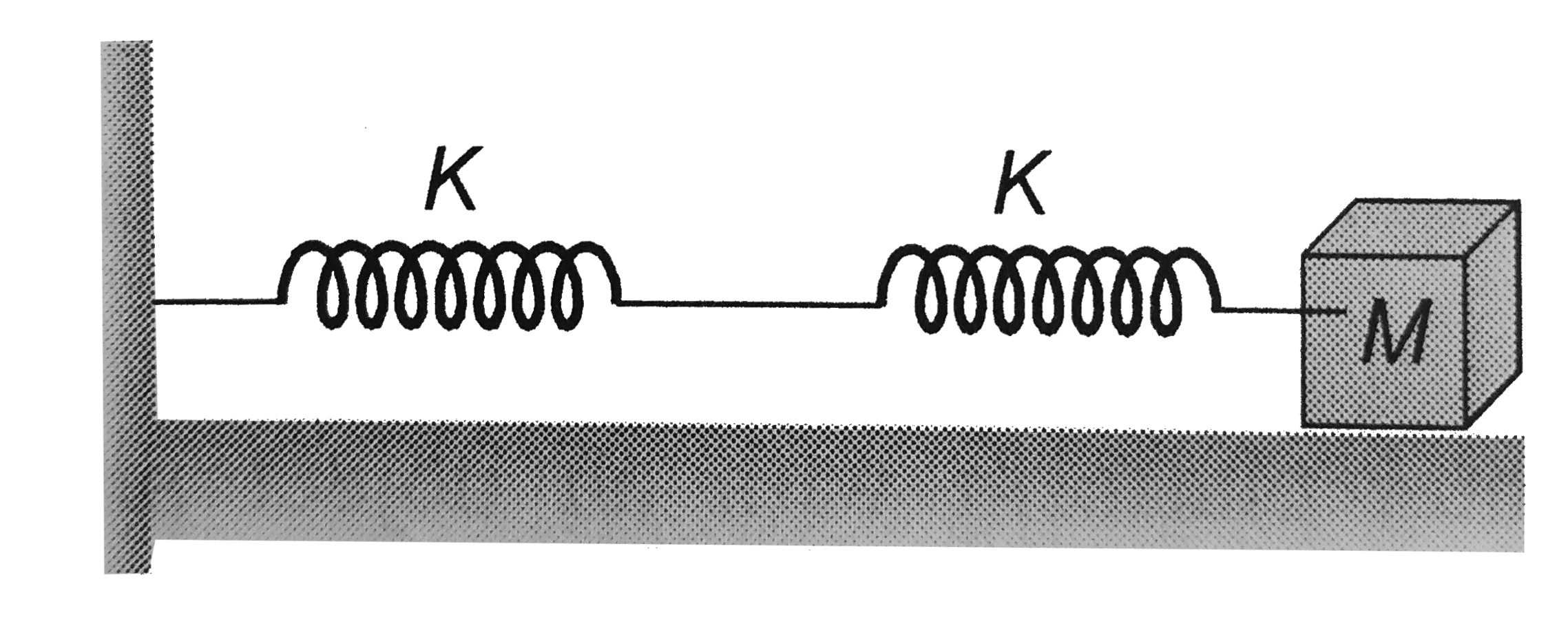 A12π√k2MB12π√kMC12π√2kMD12π√Mk
A12π√k2MB12π√kMC12π√2kMD12π√MkA block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
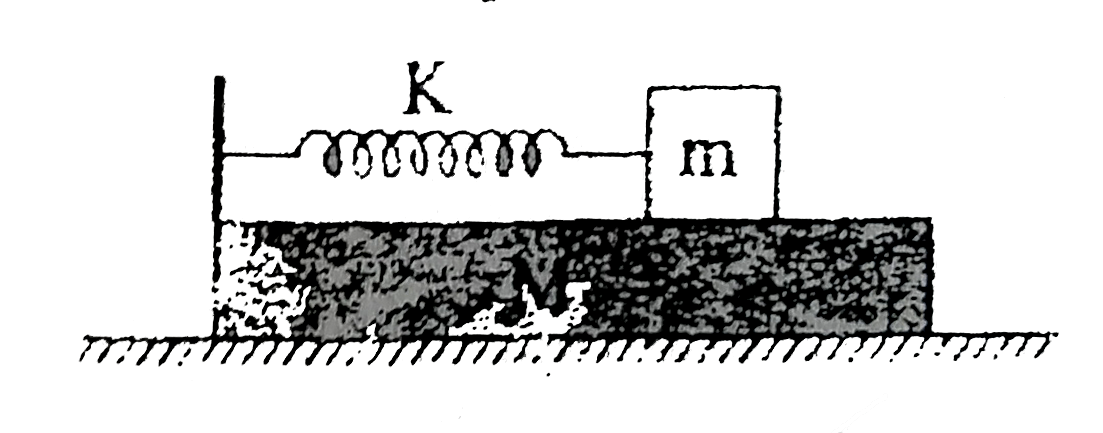 A√m2KV0B√mKv0C√2mKv0D2√mKv0
A√m2KV0B√mKv0C√2mKv0D2√mKv0A block of mass m is attached to the two springs in vertical plane as shown in the figure - 3.95. If initially both the springs are at their natural lengths then velocity of the block is maximum at displacement x given as
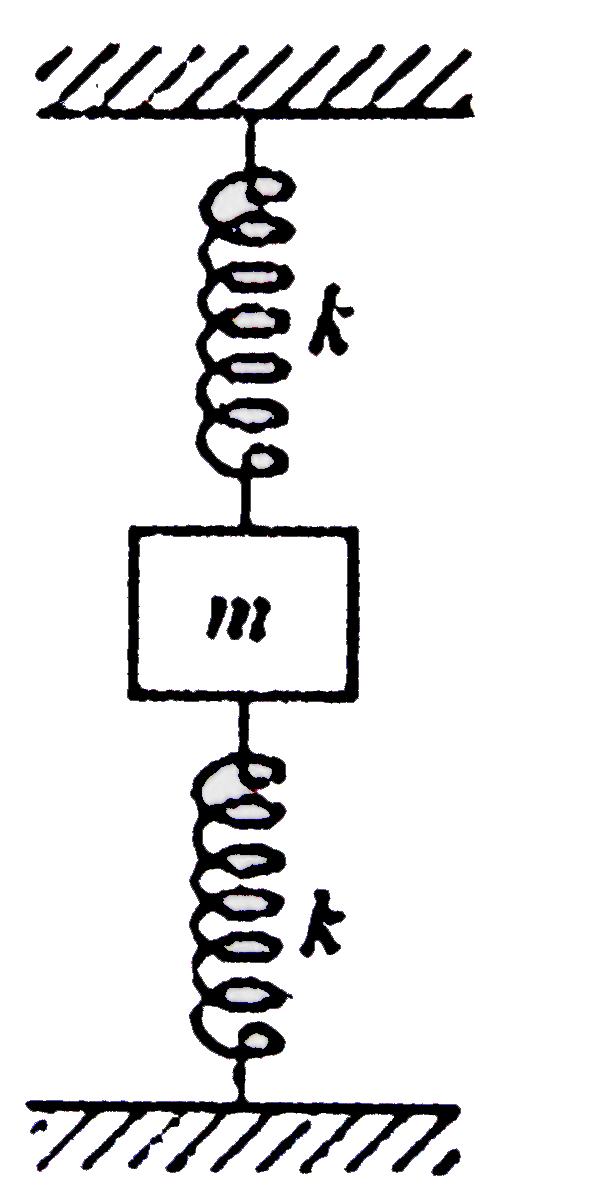 Ax=mg2kBx=mgkCx=mg4kDx=3mg2k
Ax=mg2kBx=mgkCx=mg4kDx=3mg2k
A spring elongates by 2 cm when a piece of cobalt of mass 20g is suspended from it. A water conatiner is placed below the pieces in such a way that the piece is immersed completely in water. Calculate the elongation produced in the spring.
Density of cobalt =8700kg/m3,Useg=10ms2.
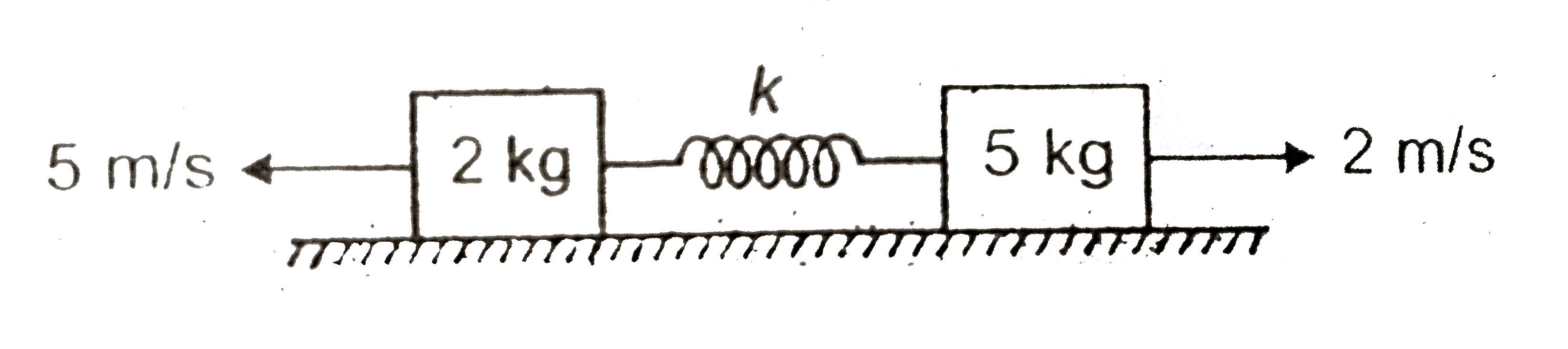
View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
View SolutionA block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View SolutionA dumbbell consists of two balls A and B of mass m=1 kg and connected by a spring. The whole system is placed on a smooth horizontal surface as shown in the figure. Initially the spring is at its natural length, the ball B is imparted a velocity v0=8√7m/s in the direction shown. The spring constant of the spring is adjusted so that the length of the spring at maximum elongation is twice that of the natural, length of the spring. Find the maximum potential energy stored (in Joule) in the spring during the motion.
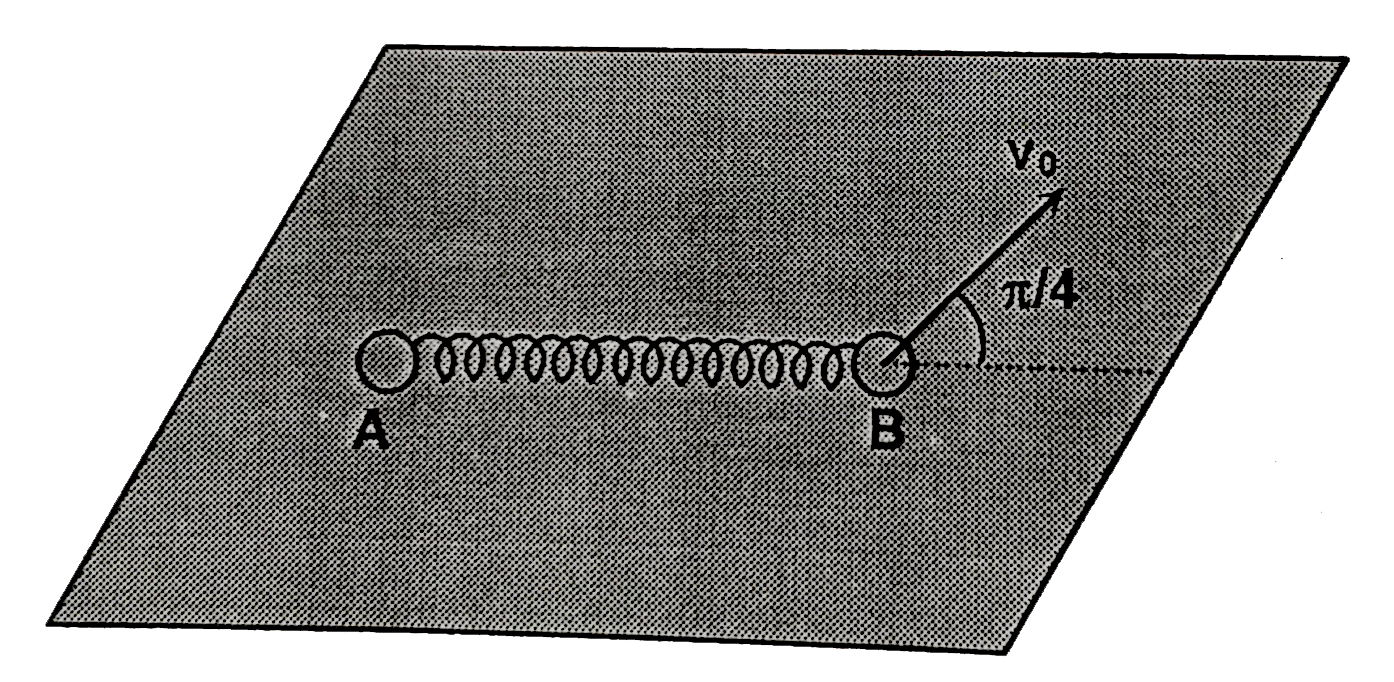
View Solution
A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)
View Solution

