The period of revolution (T) of a planet around the sun depends upon (i) radius (r ) of obit (ii) mass M of the sun and (iii) gravitational constant G. Prove that $T^{2} \propto r^{3}$

Video Solution

Text Solution

Verified by Experts

Let $T = K r^{a} M^{b} G^{c} \dots\dots (i)$
where K is a dimensionless constant
Taking dimensions on both sides of equation (i), we get
$[M^{0} L^{0} T^{1}] = {[L]}^{a} {[M]}^{b} {[M^{- 1} L^{3} T^{- 2}]}^{c}$
Comparing the exponents of M, L and T on both sides, we get
$b - c = 0, a + 3 c = 0, - 2 c = 1$
$\Rightarrow c = \frac{- 1}{2}$
$b = c = \frac{- 1}{2}$
$a = - 3 c = - 3 \times (\frac{- 1}{2}) = \frac{3}{2}$
$T = K r^{\frac{3}{2}} M^{- \frac{1}{2}} G^{- \frac{1}{2}}$
or $T^{2} = \frac{K^{2} r^{3}}{M G}$
$\Rightarrow T^{2} \propto r^{3}$
Hence proved.

Updated on:21/07/2023

The period of revolution of a planet about the sun is T. If a is radius of the circular orbit, then what is true?
A $T α a$
B $T α a^{2}$
C $T^{2} α a^{3}$
D $T^{3} α a^{2}$
Kepler's third law states that the square of period of revolution (T) of a planet around the sun, is proportional to third power of average distance, r between the sun and the planet i.e.
$T^{2} = K r^{3}$
Here, K is constant.
If masses of the sun and the planet are M and m respectively, then as per Newton's law of gravitation, force of attraction between them is $F = \frac{G M m}{r^{2}}$ where G is gravitational constant.The relation between G and K is described as
A $G K = 4 π^{2}$
B $G M K = 4 π^{2}$
C $K = G$
D $K = \frac{1}{G}$
If $T$ be the period of revolution of a plant revolving around sun in an orbit of mean radius $R$ , then identify the incorrect graph.
A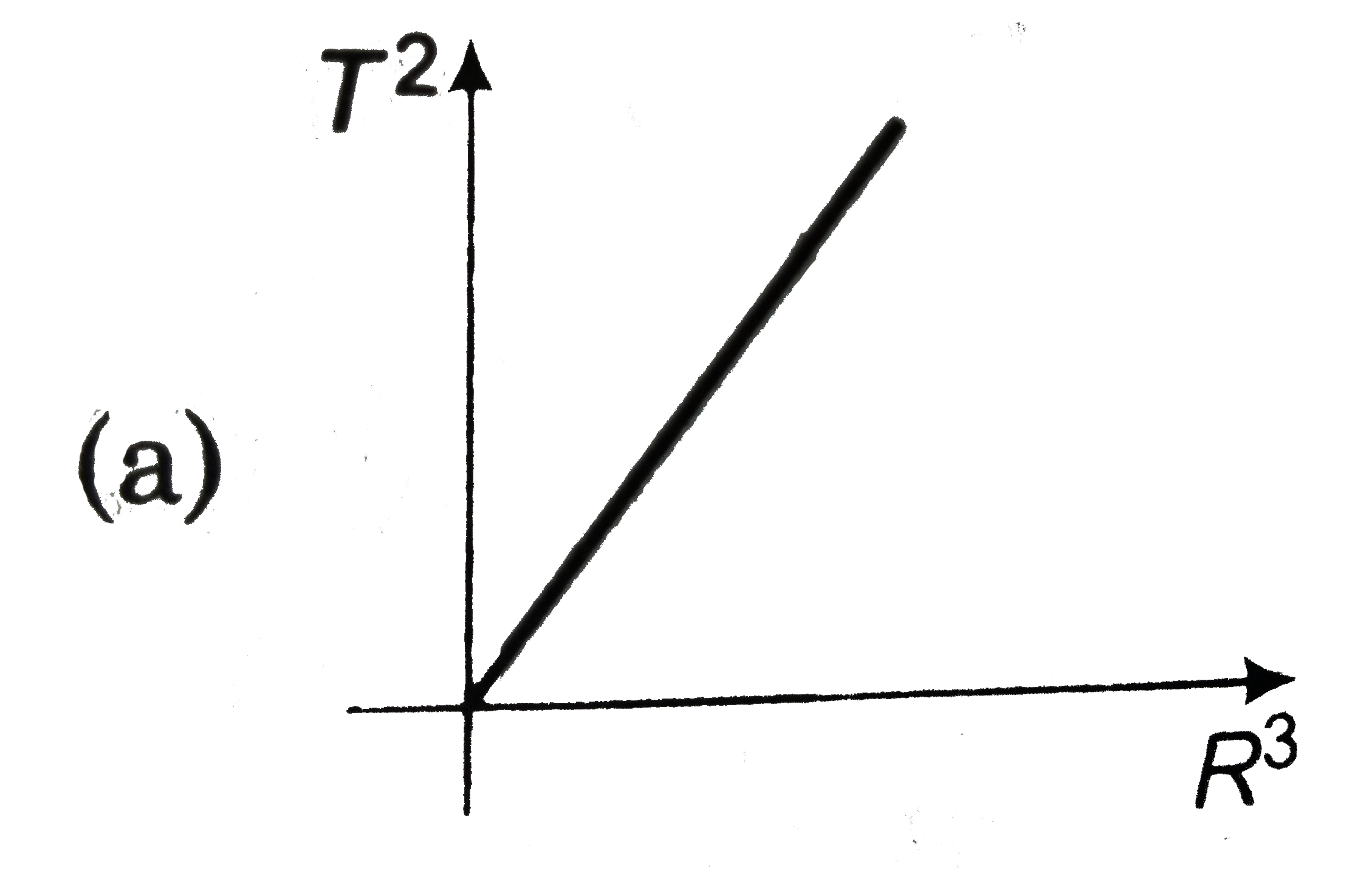
B
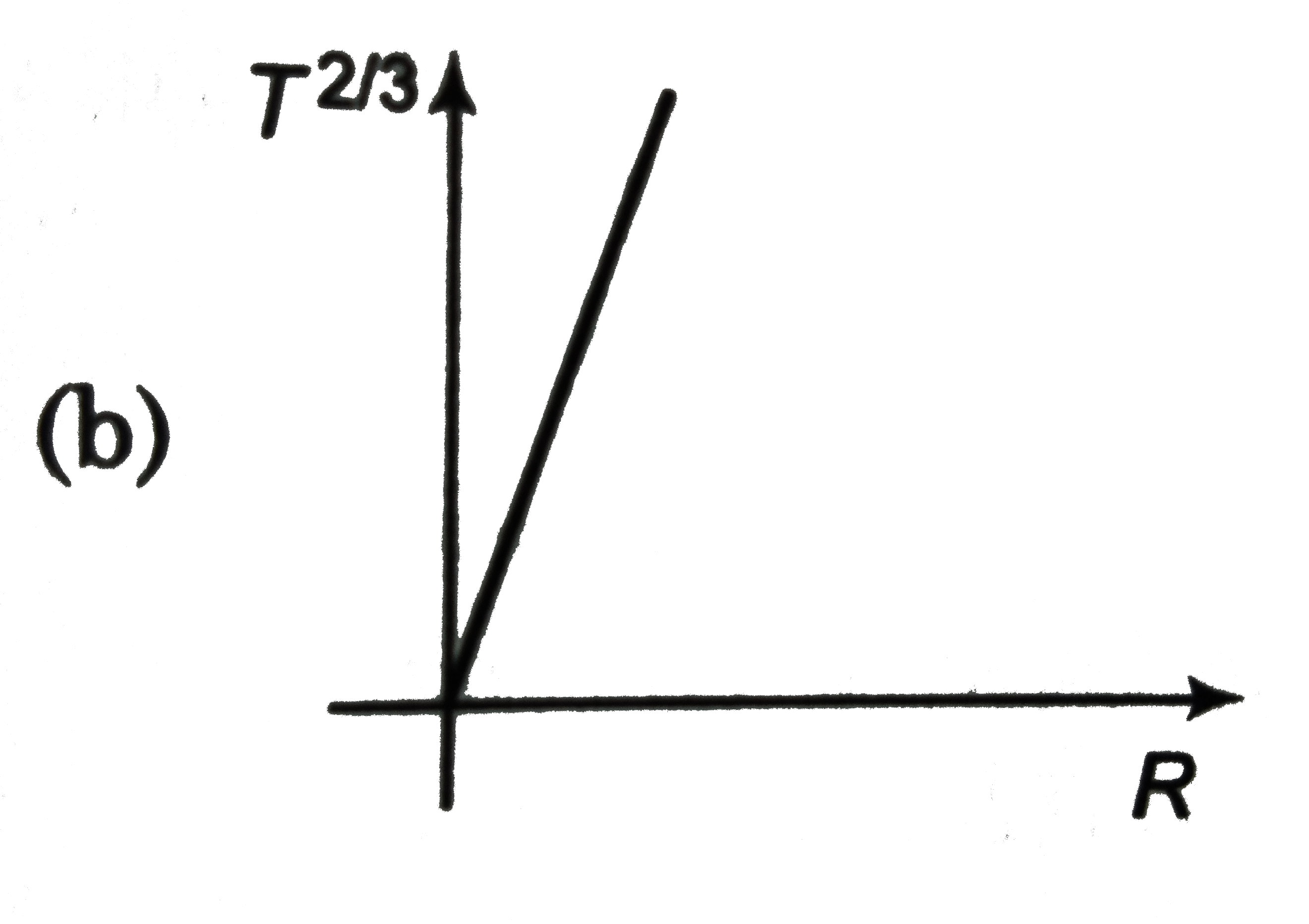C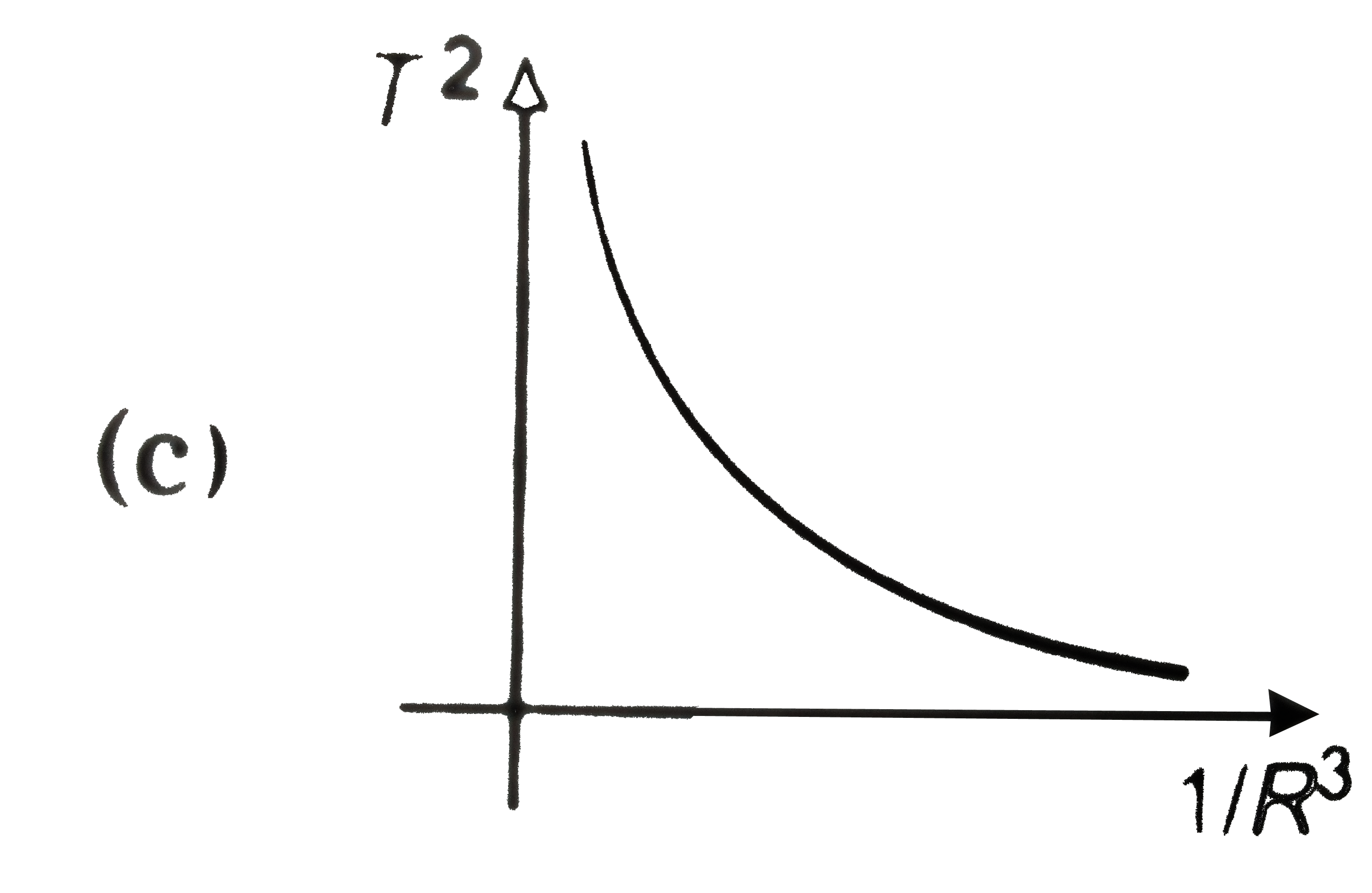
DNone of these