The period of revolution (T) of a planet around the sun depends upon (i) radius (r ) of obit (ii) mass M of the sun and (iii) gravi-tational constant G. Prove that T2∝r3
To prove that T2∝r3, we will start with Newton's law of gravitation and the concept of centripetal force. Here’s the step-by-step solution:
Step 1: Understand the forces acting on the planet
The gravitational force acting on the planet provides the necessary centripetal force for its circular motion around the Sun. The gravitational force F between the Sun and the planet is given by Newton's law of gravitation:
F=GMmr2
where:
- G is the gravitational constant,
- M is the mass of the Sun,
- m is the mass of the planet,
- r is the radius of the orbit.
Step 2: Write the expression for centripetal force
The centripetal force Fc required to keep the planet in circular motion is given by:
Fc=mv2r
where:
- v is the orbital speed of the planet.
Step 3: Set the gravitational force equal to the centripetal force
Since the gravitational force provides the centripetal force, we can set these two expressions equal to each other:
GMmr2=mv2r
Step 4: Simplify the equation
We can cancel m from both sides (assuming m≠0) and multiply both sides by r:
GMr=v2
Step 5: Relate orbital speed to the period of revolution
The orbital speed v can be expressed in terms of the period T of revolution. The relationship is given by:
v=2πrT
Step 6: Substitute v in the equation
Substituting v into the equation we derived:
GMr=(2πrT)2
Step 7: Expand and rearrange the equation
Expanding the right side gives:
GMr=4π2r2T2
Now, rearranging this equation to isolate T2:
T2=4π2r3GM
Step 8: Establish the proportionality
From the equation T2=4π2GMr3, we can see that T2 is proportional to r3:
T2∝r3
Conclusion
Thus, we have proved that the square of the period of revolution T2 is proportional to the cube of the radius of the orbit r3.
---
The gravitational force acting on the planet provides the necessary centripetal force for its circular motion around the Sun. The gravitational force F between the Sun and the planet is given by Newton's law of gravitation:
- G is the gravitational constant,
- M is the mass of the Sun,
- m is the mass of the planet,
- r is the radius of the orbit.
The centripetal force Fc required to keep the planet in circular motion is given by:
- v is the orbital speed of the planet.
Since the gravitational force provides the centripetal force, we can set these two expressions equal to each other:
We can cancel m from both sides (assuming m≠0) and multiply both sides by r:
The orbital speed v can be expressed in terms of the period T of revolution. The relationship is given by:
Substituting v into the equation we derived:
Expanding the right side gives:
From the equation T2=4π2GMr3, we can see that T2 is proportional to r3:
Thus, we have proved that the square of the period of revolution T2 is proportional to the cube of the radius of the orbit r3.
Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Conceptual Problem
Explore 65 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:NCERT Exercises
Explore 40 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:multiple choice Questions
Explore 13 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
Similar Questions
The period of revolution(T) of a planet moving round the sun in a circular orbit depends upon the radius (r) of the orbit, mass (M) of the sun and the gravitation constant (G). Then T is proportioni of ra. The value of a is
View SolutionA planet moves around the sun in nearly circular orbit. Its period of revolution 'T' depends upon :
(i) radius 'r' or orbit (ii) mass 'M' of the sum and
(iii) the gravitational constant G.
Show dimensionally that T2∝r2.
View Solution
Knowledge Check
The period of revolution of a planet about the sun is T. If a is radius of the circular orbit, then what is true?
ATαaBTαa2CT2αa3DT3αa2Kepler's third law states that the square of period of revolution (T) of a planet around the sun, is proportional to third power of average distance, r between the sun and the planet i.e.
T2=Kr3
Here, K is constant.
If masses of the sun and the planet are M and m respectively, then as per Newton's law of gravitation, force of attraction between them is F=GMmr2 where G is gravitational constant.The relation between G and K is described asAGK=4π2BGMK=4π2CK=GDK=1GIf T be the period of revolution of a plant revolving around sun in an orbit of mean radius R, then identify the incorrect graph.
A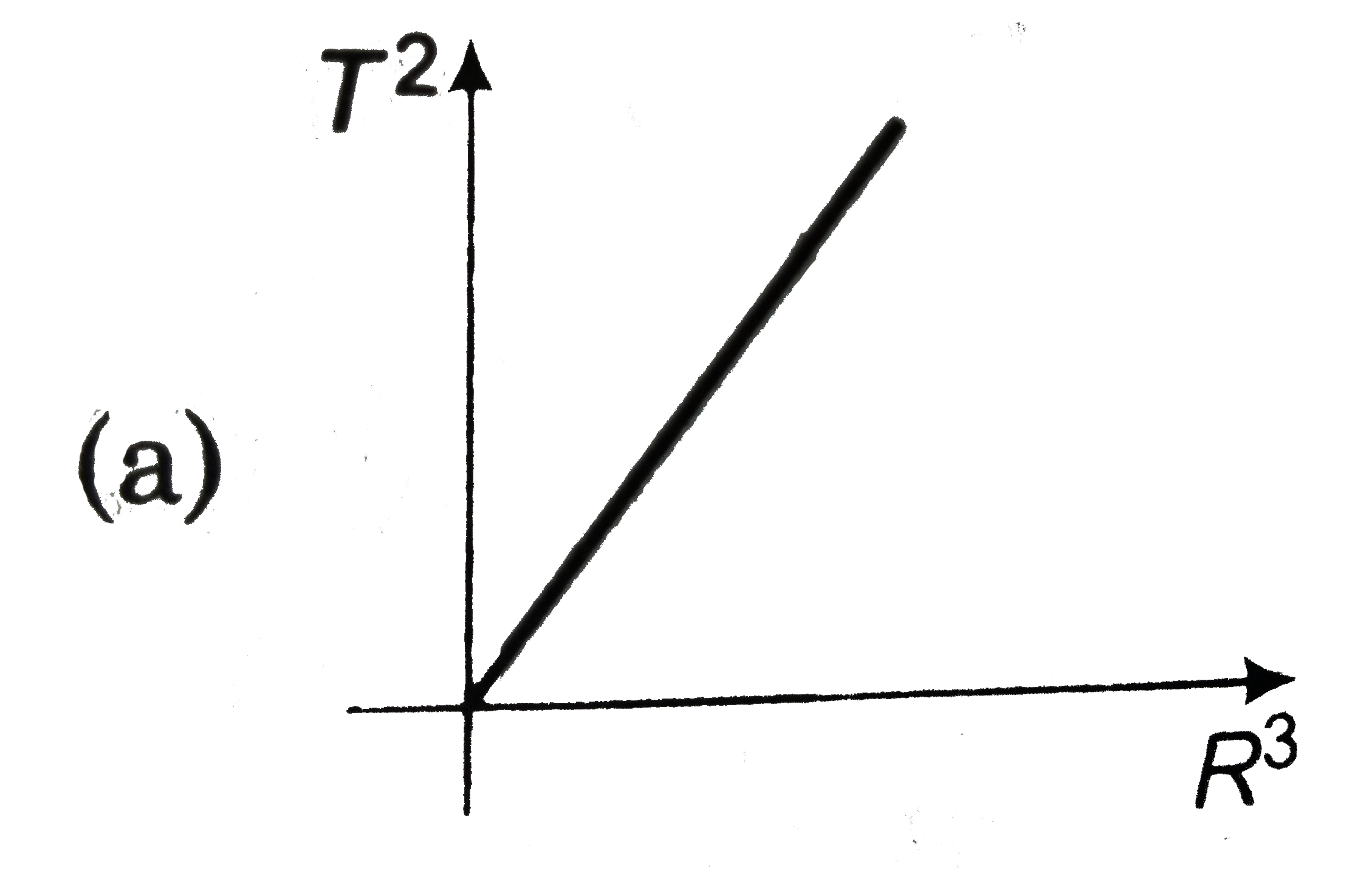 B
B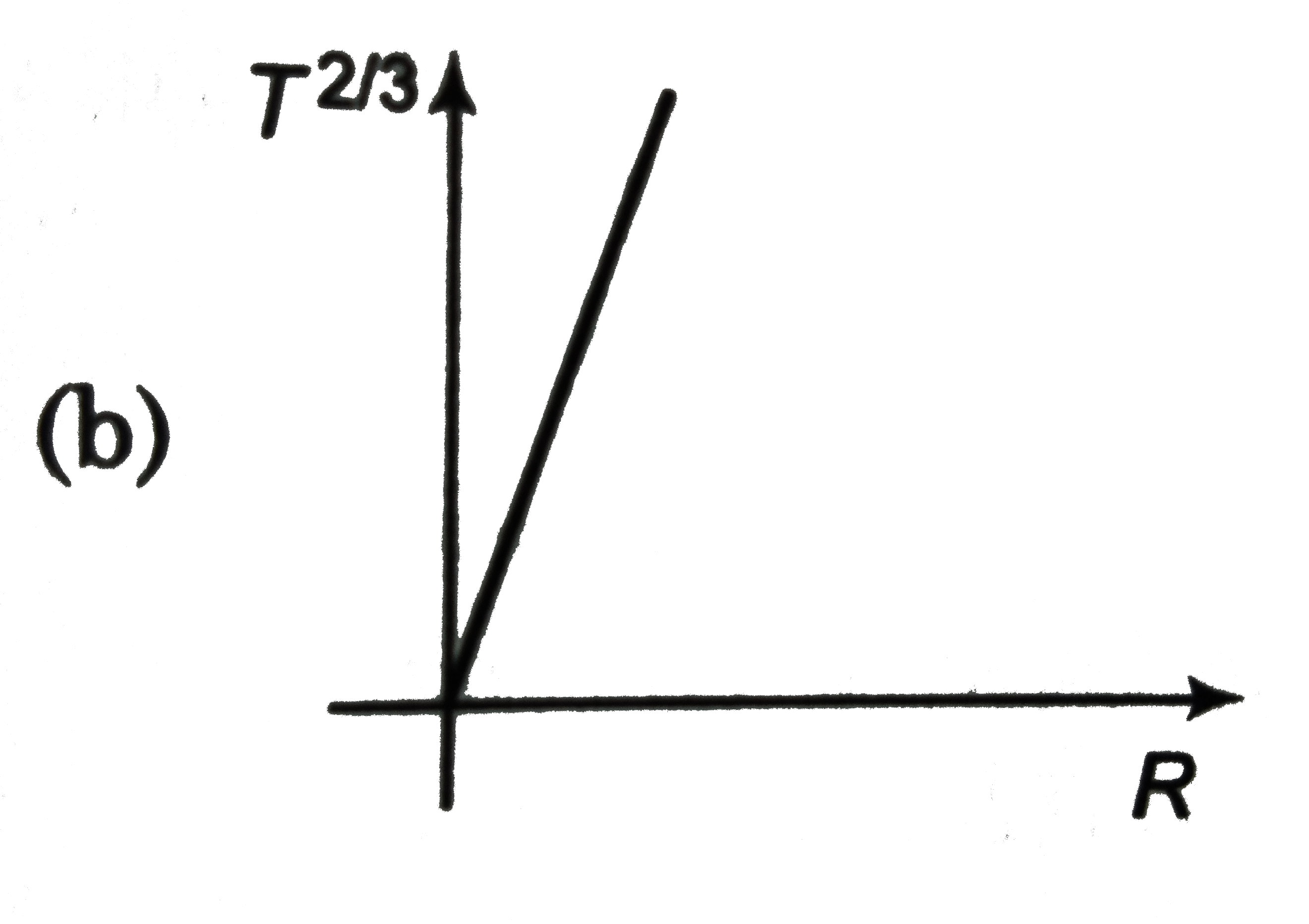 C
C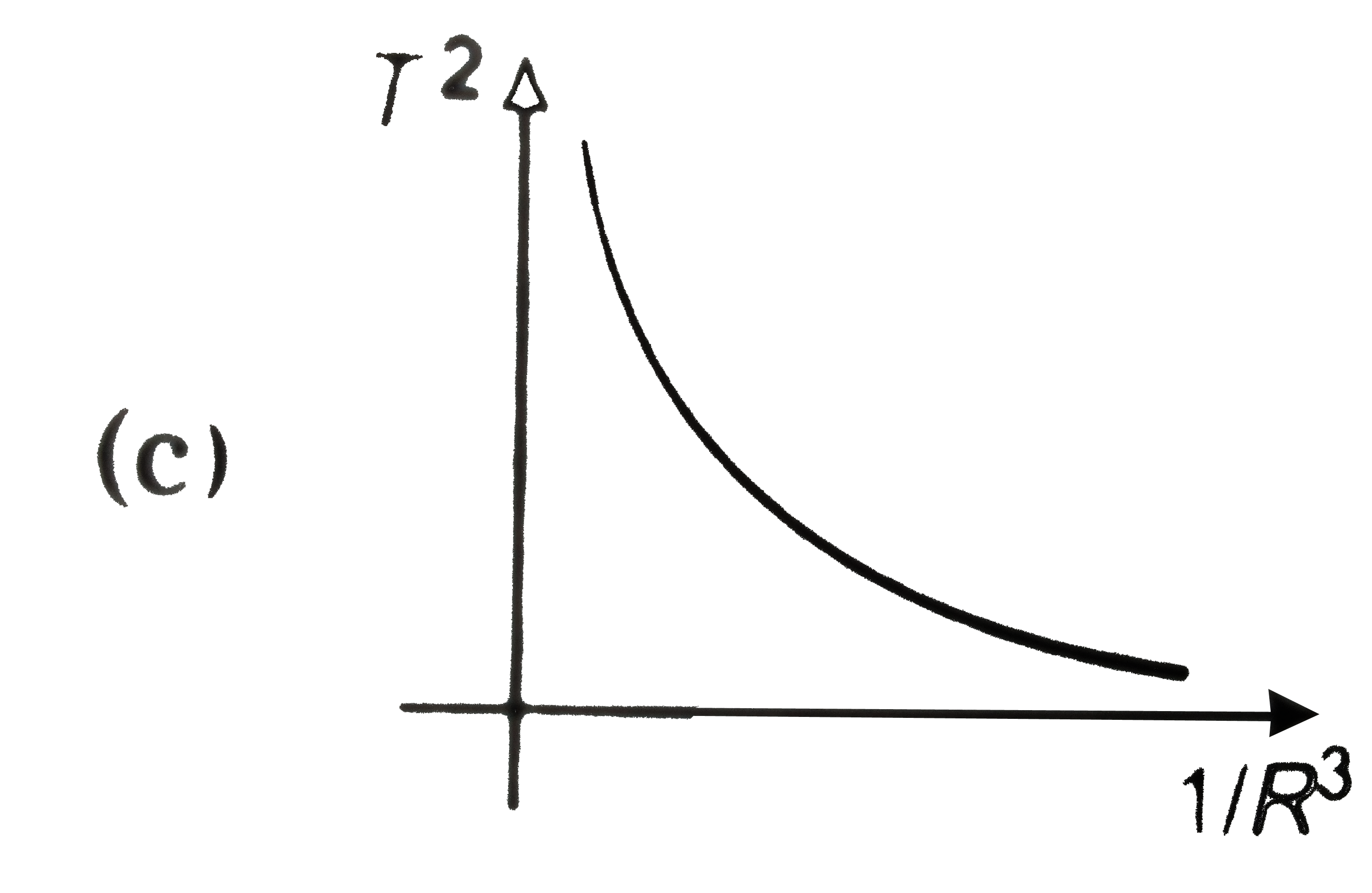 DNone of these
DNone of these
Consider a planet of mass (m), revolving round the sun. The time period (T) of revolution of the planet depends upon the radius of the orbit (r), mass of the sun (M) and the gravitational constant (G). Using dimensional analysis, verify Kepler' third law of planetary motion.
View SolutionThe period of revolution of a planet around the sun in a circular orbit is same as that of period of similar planet revolving around a star of twice the raduis of first orbit and if M is the mass of the sun then the mass of star is
View SolutionKepler's third law states that square of period revolution (T) of a planet around the sun is proportional to third power of average distance i between sun and planet i.e. T2=Kr3
here K is constant
if the mass of sun and planet are M and m respectively then as per Newton's law of gravitational the force of alteaction between them is F=GMmr2, here G is gravitational constant. The relation between G and K is described as
View SolutionKeller's third law states that the square of period of revolution (T) of a planet around the sun is proportional to the sun is proportional to the third power of average distance , r between the sun and the planet i.e T2=Kr3 Here ,K is constant . If masses of the sun and the planet are M and m respectively , then as per Newton's law of gravitation force of attraction between them is F=GMmr2 , Where G is gravitational constant . The relation between G and K is described as
View SolutionKepler's third law states that square of period revolution (T) of a planet around the sun is proportional to third power of average distance i between sun and planet i.e. T2=Kr3
here K is constant
if the mass of sun and planet are M and m respectively then as per Newton's law of gravitational the force of alteaction between them is F=GMmr2, here G is gravitational constant. The relation between G and K is described as
View Solution

