A uniform rope of mass M=0.1kg and length L=10m hangs from the celling. [g=10m/s2] :-
The correct Answer is:4
v=√xg
dxdt=√xg⇒ 10∫0dx√x=√gt∫0dt
⇒t=2 sec.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY37videos
TEST PAPER
- BOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY37videos
TEST PAPER
- BOOK - RESONANCECHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)3videos
SEQUENCE & SERIES
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS263videos
TEST PAPERS
Similar Questions
A uniform rope of mass 0.1kg and length 2.45m hangs from a ceiling.
(a) Find the speed of transverse wave in the rope at a point 0.5m distant from the lower end.
(b) Calculate the time taken by a transverse wave to travel the full length of the rope.
 View Solution
View SolutionA uniform rope of mass m and length L hangs from a celling. (a) Show that the speed of a transverse wave on the rope is a function of y, the distance from the lower end, and is given by t=2√L/g.
View Solution
Knowledge Check
- Question 1 - Select One
Find the time taken by a transverse wave to travel the full length fo a uniform rope of mass 0.1 kg and length 2.45 m hangs from the ceiling
A1 sB0.5 sC2 sD1.5 s - Question 2 - Select One
A uniform rope of mass 0.1 kg and length 2.5 m hangs from ceiling. The speed of transverse wave in the rope at upper end at a point 0.5 m distance from lower end will be
A5 ms−1and2.24ms−1B10 ms−1and3.23ms−1C7.5 ms−1and1.2ms−1DNone of these - Question 3 - Select One
An uniform rod of mass m=30kg and length l=0.80m is free to rotate about a horizontal axis O passing through its centre. A particle P of mass M=11.2kg falls vertically through a height h=36245m and collides elastically with the rod at a distance l4 from O. at the instant of collision the rod was stationary and was at angle α=37∘ with horizontal as shown in figure
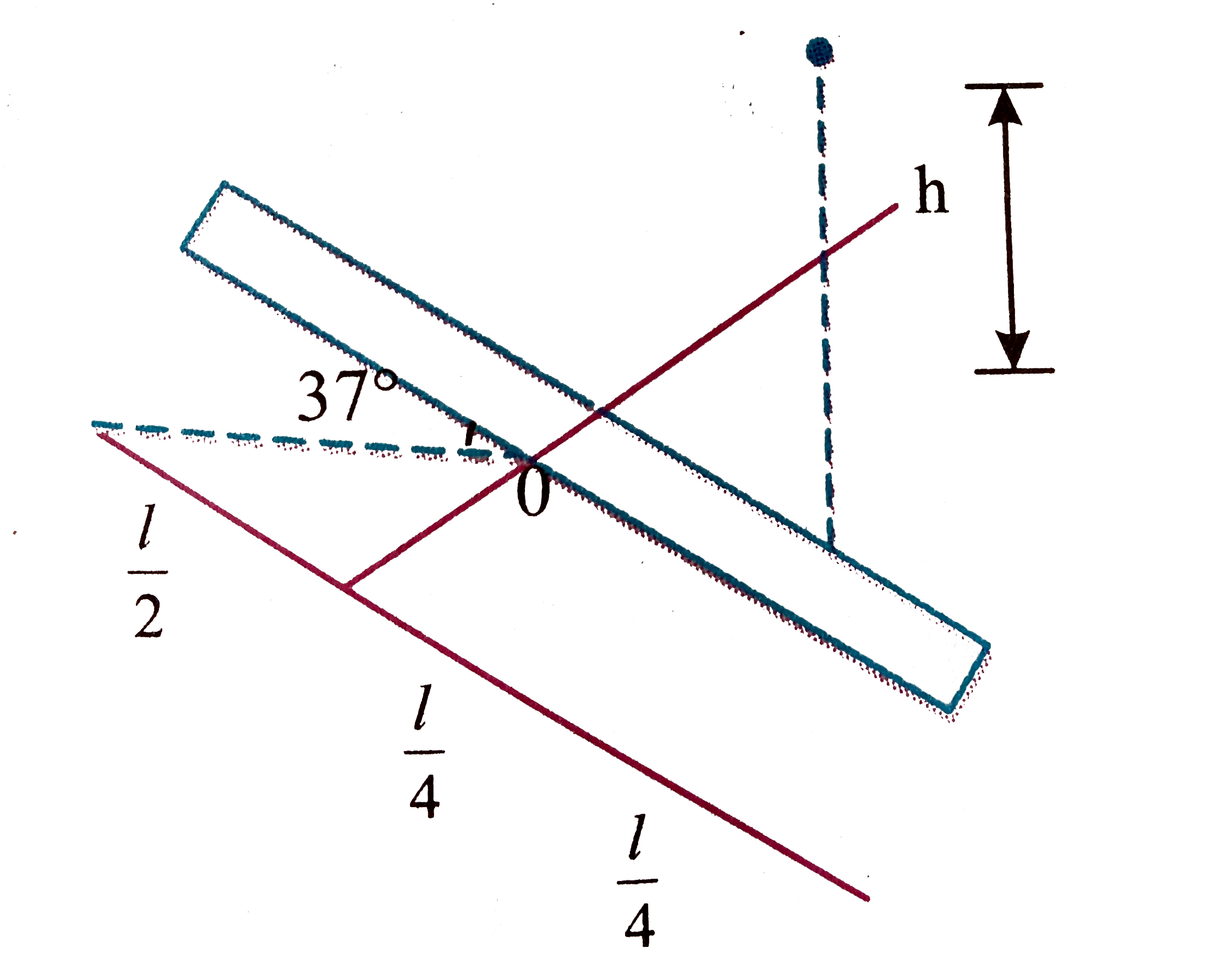
Velocity of particle P after collision (g=10ms−2)A79ms−1B7ms−1C97ms−1D1ms−1
A uniform rope of mass m and length L hangs from a ceiling. (a) Show that the speed of a transverse wave on the rope is a function of y, the distance from the lower end, and is given by v=√gy. (b) Show that the time a transverse wave takes to travel the length of the rope is given by t=2√L/g.
View Solutionthe moment of inertia of a uniform rod of mass 0.50 kg and length 1 m is 0.10 kg m^2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
View SolutionA uniform wire of length 20 m and weighing 5 kg hangs vertically. If g=10ms−2, then the speed of transverse waves in the middle of the wire is
View SolutionThe density of a uniform steel wire of mass 1.6×10−2kg, and length 2.5 m is 8×103kg/m3. When it is loaded by 8kg, it elongates by 1.25 mm. If g=10m/s2, then the Young's modulus of the material of the wire is
View SolutionA block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
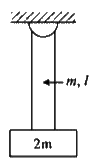
The speed of the pulseat the mid point of rope is:View Solution

