The graph of the ineequation 2x+3y≥6 does not lie in the first quadrant.(True/False)
The correct Answer is:False
To determine whether the graph of the inequality 2x+3y≥6 lies in the first quadrant, we will follow these steps:
Step 1: Rewrite the Inequality
We start with the inequality:
2x+3y≥6
Step 2: Find the Boundary Line
To analyze the inequality, we first consider the corresponding equation:
2x+3y=6
This equation represents the boundary line of the inequality.
Step 3: Find Intercepts
To plot the line, we find the x-intercept and y-intercept.
- X-intercept: Set y=0:
2x+3(0)=6⟹2x=6⟹x=3
So, the x-intercept is (3,0).
- Y-intercept: Set x=0:
2(0)+3y=6⟹3y=6⟹y=2
So, the y-intercept is (0,2).
Step 4: Plot the Line
Now we plot the points (3,0) and (0,2) on the graph. Draw a straight line through these points. Since the inequality is ≥, we will use a solid line to indicate that points on the line are included in the solution set.
Step 5: Determine the Region
To determine which side of the line satisfies the inequality 2x+3y≥6, we can test a point not on the line. A common choice is the origin (0,0):
2(0)+3(0)=0≱6
Since the origin does not satisfy the inequality, the solution set lies on the opposite side of the line.
Step 6: Analyze the Quadrants
The first quadrant is where both x and y are positive. The line divides the plane, and since the region satisfying the inequality does not include the origin, we need to check if there are points in the first quadrant that satisfy the inequality.
Step 7: Conclusion
The region defined by 2x+3y≥6 does not include any points in the first quadrant, as we can see from the graph. Therefore, the statement "The graph of the inequality 2x+3y≥6 does not lie in the first quadrant" is True.
We start with the inequality:
2x+3y≥6
To analyze the inequality, we first consider the corresponding equation:
2x+3y=6
This equation represents the boundary line of the inequality.
To plot the line, we find the x-intercept and y-intercept.
2x+3(0)=6⟹2x=6⟹x=3
So, the x-intercept is (3,0).
2(0)+3y=6⟹3y=6⟹y=2
So, the y-intercept is (0,2).
Now we plot the points (3,0) and (0,2) on the graph. Draw a straight line through these points. Since the inequality is ≥, we will use a solid line to indicate that points on the line are included in the solution set.
To determine which side of the line satisfies the inequality 2x+3y≥6, we can test a point not on the line. A common choice is the origin (0,0):
2(0)+3(0)=0≱6
Since the origin does not satisfy the inequality, the solution set lies on the opposite side of the line.
The first quadrant is where both x and y are positive. The line divides the plane, and since the region satisfying the inequality does not include the origin, we need to check if there are points in the first quadrant that satisfy the inequality.
The region defined by 2x+3y≥6 does not include any points in the first quadrant, as we can see from the graph. Therefore, the statement "The graph of the inequality 2x+3y≥6 does not lie in the first quadrant" is True.
Topper's Solved these Questions
- LINEAR PROGRAMMING Book:MODERN PUBLICATIONChapter:LINEAR PROGRAMMING Exercise:Chapter Test
Explore 12 Videos
- LINEAR PROGRAMMING Book:MODERN PUBLICATIONChapter:LINEAR PROGRAMMING Exercise:Revision Exercise
Explore 17 Videos
- INVERSE - TRIGONOMETRIC FUNCTIONSBook:MODERN PUBLICATIONChapter:INVERSE - TRIGONOMETRIC FUNCTIONSExercise:CHAPTER TEST (2)
Explore 11 Videos
- MATRICESBook:MODERN PUBLICATIONChapter:MATRICESExercise:CHAPTER TEST (3)
Explore 12 Videos
Similar Questions
Knowledge Check
The solution set formed by the inequations x+y≥3,x+y≤4,x≤2 in the first quadrant represents a
AtriangleBparallelogramCrectangleDrhombusThe graph of 2x−3≥0 is
A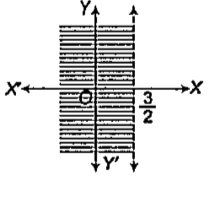 B
B C
C D
D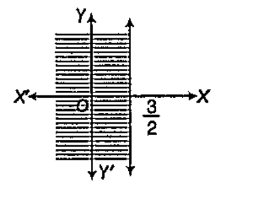
The area of the region bounded by x2=y−2,y=4,y=6 and the Y-axis in the first quadrant is
A23B23(8−√2)C23(8−2√2)D32(8−√2)
2x+y≥6
View SolutionSketch the graph of the function y=6x−x2. Determined the total area in the first quadrant between the curve and the y-axis.
View SolutionState True or False :
The Graphical solution set of the inequation 0≤y,x≥0 lies in second quadrant.
View Solution−3x+2y≥−6
View SolutionThe area of the region bounded by the curve y2=xand the Y axis in the first quadrant and lines y=3andy=9 is ______
View Solution

