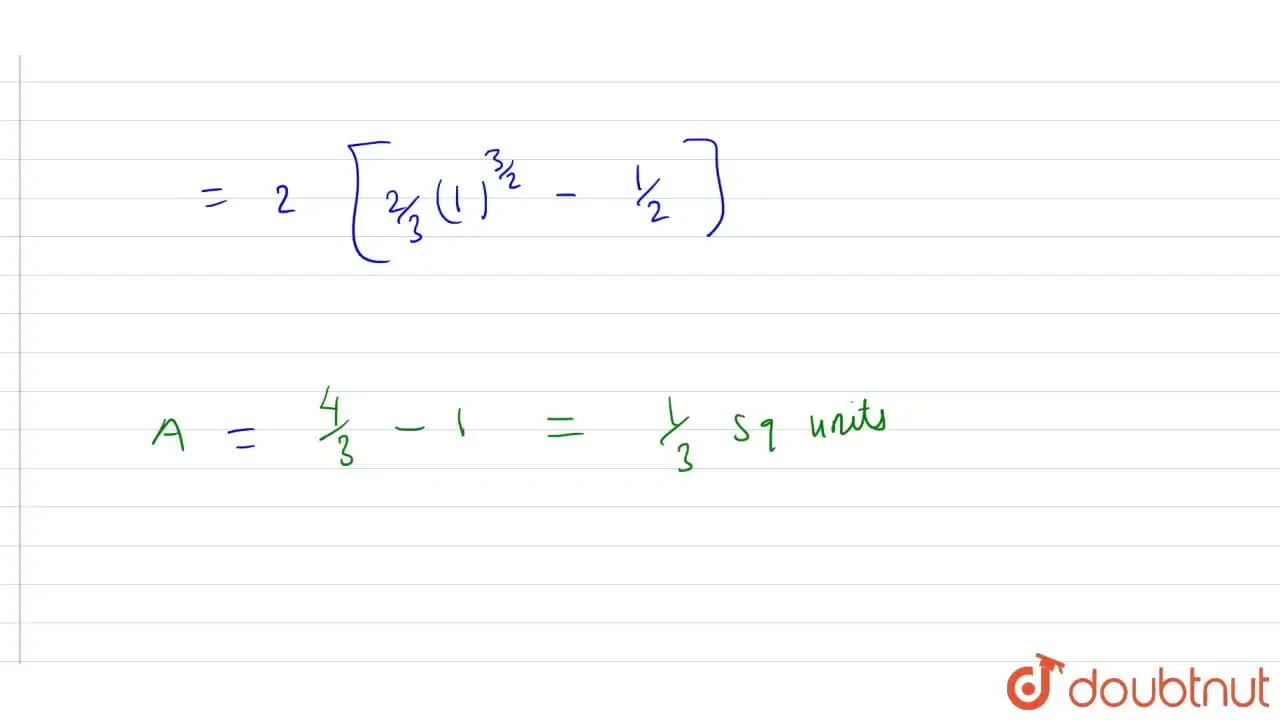Draw a rough sketch of the region enclosed between the curve y2=4x and the line y=2x. Also, determine the area of the region.
The correct Answer is:13 sq. units. 3
Step by step video, text & image solution for Draw a rough sketch of the region enclosed between the curve y ^(2) = 4x and the line y = 2x. Also, determine the area of the region. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - OBJECTIVE TYPE QUESTIONS20videos
APPLICATIONS OF THE INTEGRALS
- BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - OBJECTIVE TYPE QUESTIONS -FILL IN THE BLANKS5videos
APPLICATIONS OF THE INTEGRALS
- BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - EXERCISE 8 (A)28videos
APPLICATIONS OF THE INTEGRALS
- BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - CHAPTER TEST (1)12videos
APPLICATIONS OF DERIVATIVES
- BOOK - MODERN PUBLICATIONCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - CHAPTER TEST12videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
Area enclosed between the curve y2=x and the line y = x is
View SolutionArea enclosed between the curve y=x2 and the line y = x is
View SolutionArea of the region enclosed between the curve x=1−y2 and the Y-axis is
View SolutionDraw a rough sketch to indicate the region bounded between the curve y2=4ax and the line x=3. also, find the area of this region.
View SolutionWhat is the area of the region enclosed between the curve y2=2x and the straight line y=x?
View SolutionArea of the region between the curve y=x2−3x and the line y = 2x is
View SolutionArea of the region bounded by the curve y2= 4x , y-axis and the line y = 3 is (A) 2 (B) 94 (C) 93 (D) 92
View SolutionThe area of the region bouned by the curve y=2x−x2 and the line y=x is
View SolutionThe area of the region bouned by the curve y=2x−x2 and the line y=x is
View SolutionThe area of the region bounded by the curve y=x2 and the line y=16 is :
View Solution