Consider the fractions:
(a) Find their graphs and shade the closed region between them
(b) Find the area of their shaded region.
The correct Answer is:2 sq. units
To solve the problem step by step, we will first find the graphs of the functions f(x)=|x|−1 and g(x)=1−|x|, then we will shade the region between them and finally calculate the area of the shaded region.
Step 1: Graphing f(x)=|x|−1
1. Understanding the function: The function f(x)=|x|−1 represents the absolute value function shifted down by 1 unit.
2. Finding key points:
- At x=0: f(0)=|0|−1=−1 (Point: (0,−1))
- At x=1: f(1)=|1|−1=0 (Point: (1,0))
- At x=−1: f(−1)=|−1|−1=0 (Point: (−1,0))
3. Graphing: The graph will have a V-shape, opening upwards, with the vertex at (0,−1) and intersecting the x-axis at (1,0) and (−1,0).
Step 2: Graphing g(x)=1−|x|
1. Understanding the function: The function g(x)=1−|x| represents the absolute value function reflected over the x-axis and shifted up by 1 unit.
2. Finding key points:
- At x=0: g(0)=1−|0|=1 (Point: (0,1))
- At x=1: g(1)=1−|1|=0 (Point: (1,0))
- At x=−1: g(−1)=1−|−1|=0 (Point: (−1,0))
3. Graphing: The graph will also have a V-shape, opening downwards, with the vertex at (0,1) and intersecting the x-axis at (1,0) and (−1,0).
Step 3: Shading the Region Between the Graphs
1. Identifying the region: The area between f(x) and g(x) lies between the points where both functions intersect, which is at x=−1 and x=1.
2. Shading the area: The region between the two graphs from x=−1 to x=1 is the area we need to calculate.
Step 4: Finding the Area of the Shaded Region
1. Setting up the integral: The area A between the curves from x=−1 to x=1 can be found using the integral:
A=∫1−1(g(x)−f(x))dx
Substitute g(x) and f(x):
A=∫1−1((1−|x|)−(|x|−1))dx
Simplifying the integrand:
A=∫1−1(2−2|x|)dx
2. Calculating the integral: Since the function is even, we can calculate from 0 to 1 and double it:
A=2∫10(2−2x)dx
=2(2x−x2)10=2((2⋅1−12)−(2⋅0−02))
=2(2−1)=2⋅1=2
Final Answer
The area of the shaded region between the two graphs is 2 square units.
---
2. Finding key points:
- At x=0: f(0)=|0|−1=−1 (Point: (0,−1))
- At x=1: f(1)=|1|−1=0 (Point: (1,0))
- At x=−1: f(−1)=|−1|−1=0 (Point: (−1,0))
3. Graphing: The graph will have a V-shape, opening upwards, with the vertex at (0,−1) and intersecting the x-axis at (1,0) and (−1,0).
2. Finding key points:
- At x=0: g(0)=1−|0|=1 (Point: (0,1))
- At x=1: g(1)=1−|1|=0 (Point: (1,0))
- At x=−1: g(−1)=1−|−1|=0 (Point: (−1,0))
3. Graphing: The graph will also have a V-shape, opening downwards, with the vertex at (0,1) and intersecting the x-axis at (1,0) and (−1,0).
2. Shading the area: The region between the two graphs from x=−1 to x=1 is the area we need to calculate.
A=∫1−1(g(x)−f(x))dx
Substitute g(x) and f(x):
A=∫1−1((1−|x|)−(|x|−1))dx
Simplifying the integrand:
A=∫1−1(2−2|x|)dx
A=2∫10(2−2x)dx
=2(2x−x2)10=2((2⋅1−12)−(2⋅0−02))
=2(2−1)=2⋅1=2
Topper's Solved these Questions
- APPLICATIONS OF THE INTEGRALS Book:MODERN PUBLICATIONChapter:APPLICATIONS OF THE INTEGRALS Exercise:OBJECTIVE TYPE QUESTIONS
Explore 20 Videos
- APPLICATIONS OF THE INTEGRALS Book:MODERN PUBLICATIONChapter:APPLICATIONS OF THE INTEGRALS Exercise:OBJECTIVE TYPE QUESTIONS -FILL IN THE BLANKS
Explore 5 Videos
- APPLICATIONS OF THE INTEGRALS Book:MODERN PUBLICATIONChapter:APPLICATIONS OF THE INTEGRALS Exercise:EXERCISE 8 (A)
Explore 28 Videos
- APPLICATIONS OF DERIVATIVESBook:MODERN PUBLICATIONChapter:APPLICATIONS OF DERIVATIVESExercise:CHAPTER TEST (1)
Explore 12 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:MODERN PUBLICATIONChapter:CONTINUITY AND DIFFERENTIABILITYExercise:CHAPTER TEST
Explore 12 Videos
Similar Questions
Find the area of the shaded region.
View SolutionFind the area of the shaded region.
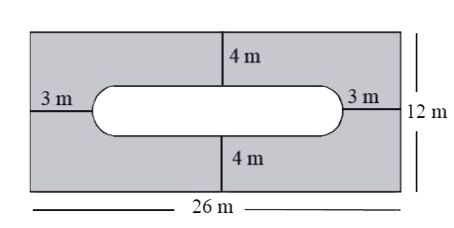
View SolutionFind the area of the shaded region:
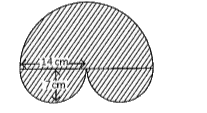
View SolutionFind the area of the shaded region :
View SolutionFind the area of the shaded regions.

View SolutionFind the area of the shaded region in
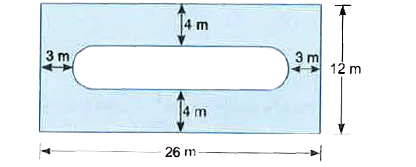
View Solution21. Find the area of the shaded region i
View SolutionFind the area of shaded region.
View SolutionFind the area of shaded region

View SolutionFind the area of shaded region
View Solution