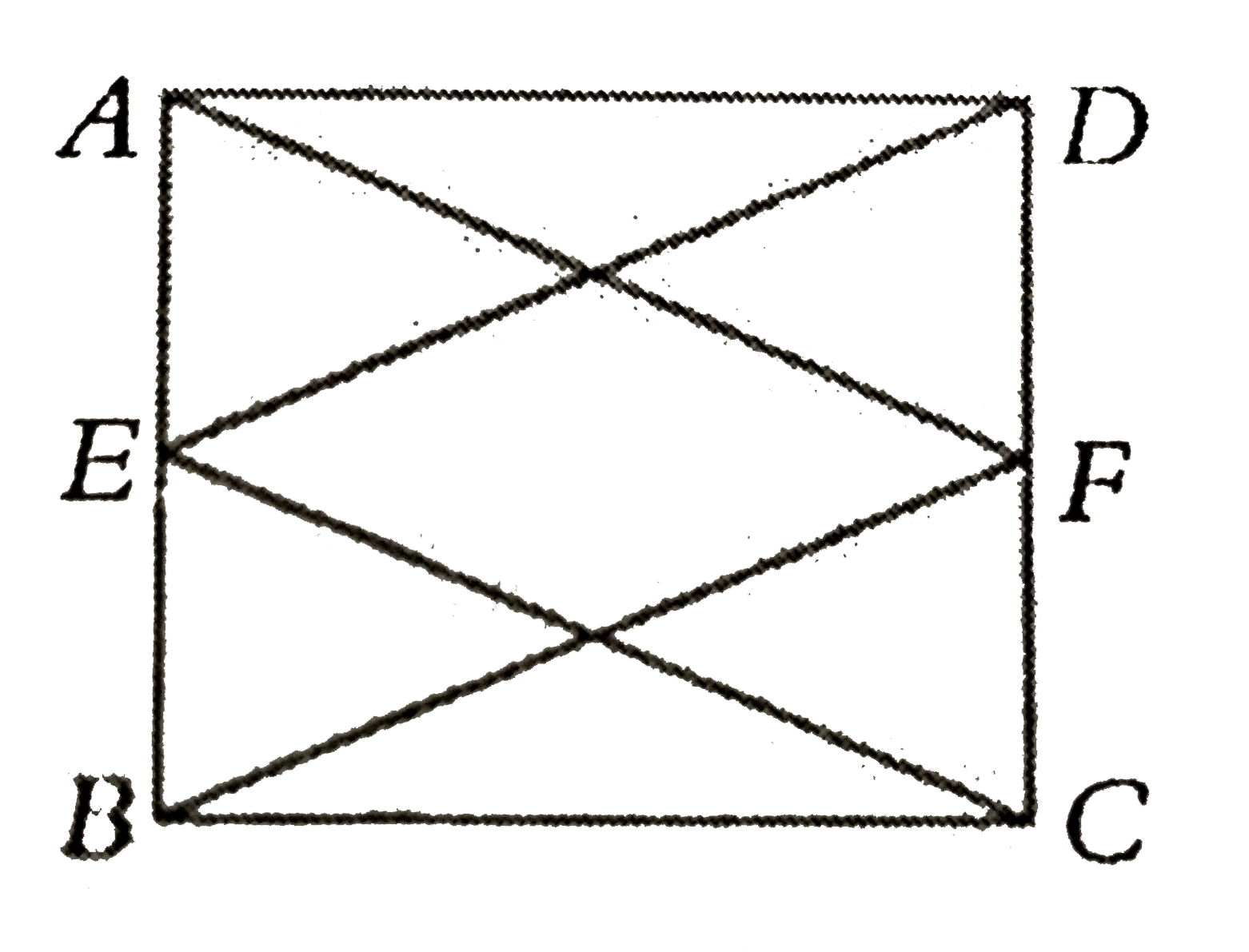
In the above figure (not to scale), E and F are the mid points of AB and CD respectively.
¯¯¯¯¯¯AB∣∣∣∣¯¯¯¯¯¯CD,¯¯¯¯¯¯BC∣∣∣∣¯¯¯¯¯¯AD,∠ADE=70∘, AND ∠BCE=40∘,∠DEC is
A
70∘
B
40∘
C
110∘
D
120∘
Video Solution
Text Solution
The correct Answer is:c
(i) Join E and F . Alternate angles are equal.
(ii) Draw a line parallel to ¯¯¯¯¯¯AD and ¯¯¯¯¯¯BC through E and F.
(iii) Find angles CEF and DEF using alternate angles property .
(iv) The sum of above is ∠DEC.
|
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 2
20 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 3
7 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Essay type Question
3 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
Knowledge Check

In the above figure (not to scale), E and F are the mid points of AB and CD respectively.
¯¯¯¯¯¯AB∣∣∣∣¯¯¯¯¯¯CD,¯¯¯¯¯¯BC∣∣∣∣¯¯¯¯¯¯AD,∠ADE=70∘, AND ∠BCE=40∘,∠DEC isA70∘B40∘C110∘D120∘ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2If D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
A2(¯¯¯¯¯¯AD−¯¯¯¯¯¯BD)B2(¯¯¯¯¯¯DC−¯¯¯¯¯¯BD)C2(¯¯¯¯¯¯BD−¯¯¯¯¯¯CA)D2(¯¯¯¯¯¯BD−¯¯¯¯¯¯AC)

In the above figure (not to scale), O is the centre of the circle. ¯¯¯¯¯¯BC and ¯¯¯¯¯¯CD are equal chords. If ∠OBC=70∘ , then find ∠BAD.
View SolutionIf a,b∈N, PQRS is a square and P, Q, R, S are mid points of AB, AD, CD, BC respectively then a+b is
View SolutionM and N are mid-point of the diagnols AC and BD respectivley of quadrilateral ABCD, then¯¯¯¯¯¯AB+¯¯¯¯¯¯AD+¯¯¯¯¯¯CB+¯¯¯¯¯¯CD=
View SolutionIf ABCD is a square then,
2¯¯¯¯¯¯AB+4¯¯¯¯¯¯BC+5¯¯¯¯¯¯CD+7¯¯¯¯¯¯DA=
View SolutionIf AD , BE and CF are medians of ΔABC, then ¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF =
View Solution

