If ABCD is a square then,
2¯¯¯¯¯¯AB+4¯¯¯¯¯¯BC+5¯¯¯¯¯¯CD+7¯¯¯¯¯¯DA=
2¯¯¯¯¯¯BD
3¯¯¯¯¯¯CA
5¯¯¯¯¯¯DB
2¯¯¯¯¯¯AC
The correct Answer is:B
Step by step video, text & image solution for If ABCD is a square then, 2bar(AB)+4bar(BC)+5bar(CD)+7bar(DA)= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - VECTORSEXERCISE - PREVIOUS YEARS MHT-CET EXAM QUESTIONS10videos
VECTORS
- BOOK - MARVEL PUBLICATIONCHAPTER - VECTORSEXERCISE - TEST YOUR GRASP20videos
VECTORS
- BOOK - MARVEL PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - TEST YOUR GRASP: CHAPTER 3-3.313videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABCD is a square, then
¯¯¯¯¯¯AB+2¯¯¯¯¯¯BC+3¯¯¯¯¯¯CD+4¯¯¯¯¯¯DA =A4 ¯¯¯¯¯¯ACB3 ¯¯¯¯¯¯ACC2 ¯¯¯¯¯¯CAD¯¯¯¯¯¯AC - Question 2 - Select One
If ABCDE is a regular penatagon then :
¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AD+¯¯¯¯¯¯ED+¯¯¯¯¯¯AE=A¯¯¯¯¯¯AC−2¯¯¯¯¯¯DCB3¯¯¯¯¯¯AC−2¯¯¯¯¯¯DCC¯¯¯¯¯¯CA−¯¯¯¯¯¯DCD3¯¯¯¯¯¯AC−¯¯¯¯¯¯DC - Question 3 - Select One
If ABCDE is a pentagon, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED=
A¯¯¯¯¯¯ACB2¯¯¯¯¯¯ACC2¯¯¯¯¯¯ADD3¯¯¯¯¯¯AD
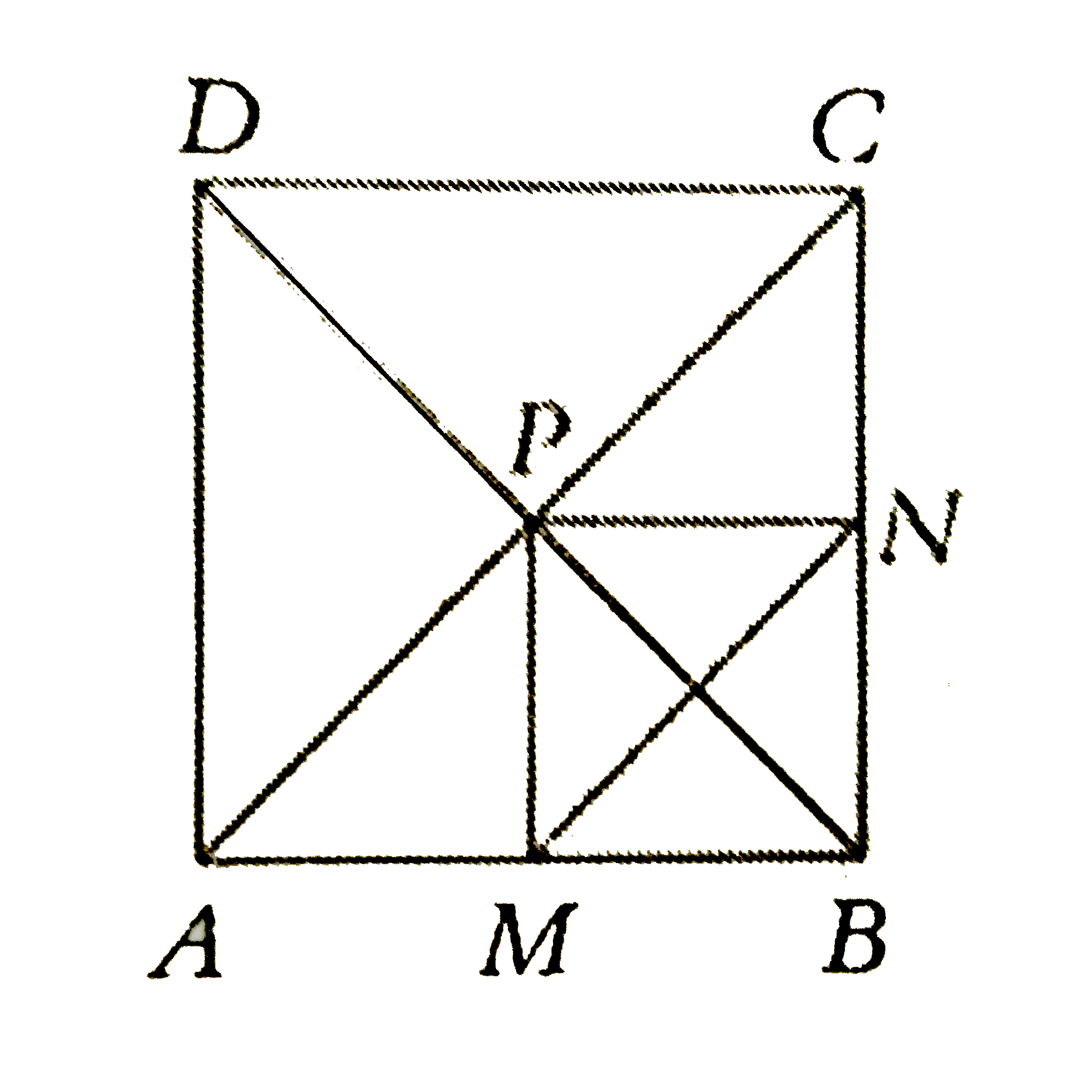
In the figure above, ABCD is a square of side 18 cm and ¯¯¯¯¯¯PN⊥¯¯¯¯¯¯BCand¯¯¯¯¯¯¯PM⊥¯¯¯¯¯¯AB. Find the length of MN.View SolutionIn the figure 11.34, ABCD is a quadrilateral in which ¯¯¯¯¯¯AB=¯¯¯¯¯¯ADand¯¯¯¯¯¯BC=¯¯¯¯¯¯DC. Diagonals ¯¯¯¯¯¯ACandBD intersect each other at O.Show that-
View Solution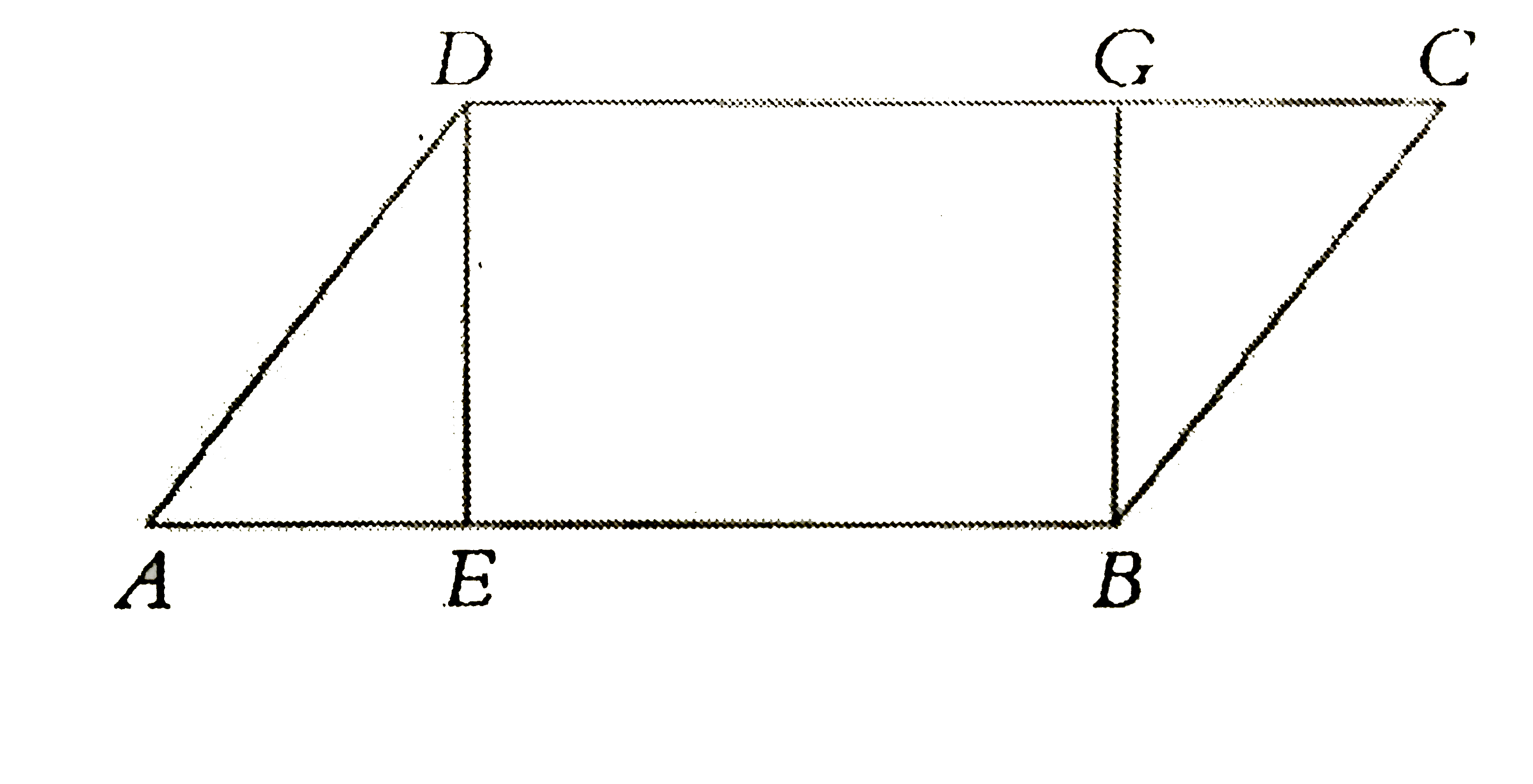
In the figure above, ABCD is a parallelogram, ¯¯¯¯¯¯BE⊥¯¯¯¯¯¯AB,¯¯¯¯¯¯BG⊥¯¯¯¯¯¯CD, and EBGD is a square. If BG=12 cm and BC=13 cm , then find AB.View Solution-
In the figure above, ABCD is a square of side 18 cm and ¯¯¯¯¯¯PN⊥¯¯¯¯¯¯BCand¯¯¯¯¯¯¯PM⊥¯¯¯¯¯¯AB. Find the length of MN.View Solution M and N are mid-point of the diagnols AC and BD respectivley of quadrilateral ABCD, then¯¯¯¯¯¯AB+¯¯¯¯¯¯AD+¯¯¯¯¯¯CB+¯¯¯¯¯¯CD=
View Solution