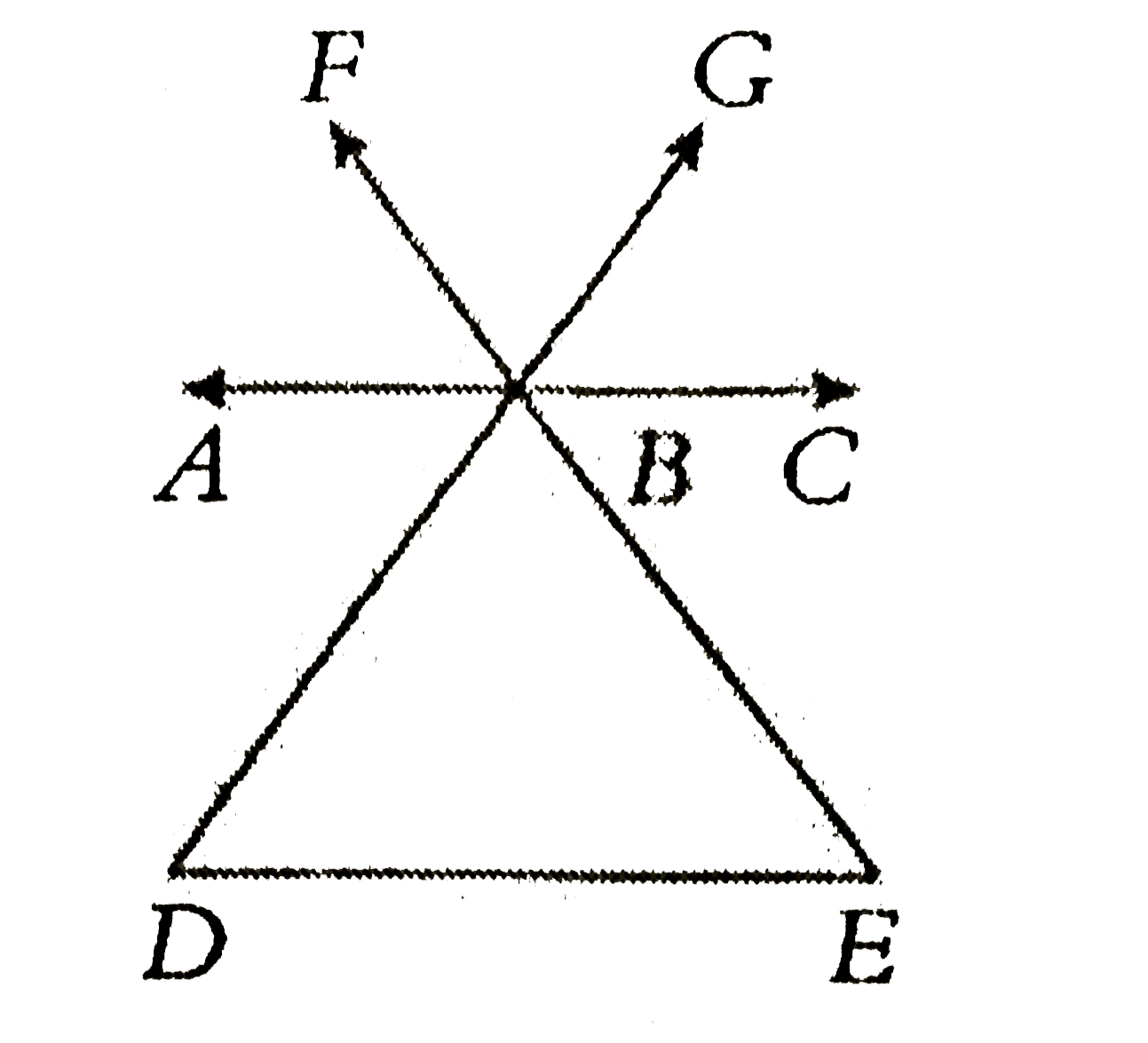
In the adjacent figure, BDE is a triangle in which EB is produced to F and DB is produced to G. If $∠ D B E = x^{\circ} = ∠ F B G = {(x + 2)}^{\circ}$ and $∠ B E D = {(x + 7)}^{\circ}$ , then the value of x is

Video Solution

Text Solution

Verified by Experts

(a) Vertically opposite angles are equal. Sum of the angles of a triangle is $180^{\circ}$ .
(b) $∠ F B G = ∠ D B E$ as they are vertically opposite angles.
(c ) Sum of three angle of $Δ D B E$ is $180^{\circ}$ . Use this to find the required angle.

Updated on:21/07/2023

If $f : R \to R and g : R \to R$ are defined by $f (x) = (2 x + 3) and g (x) = x^{2} + 7$ , then the values of x such that g(f(x))=8 are
A1,2
B $- 1, 2$
C $- 1, - 2$
D $1, - 2$
If $f : R \to R and g : R \to R$ are defined by $f (x) = 2 x + 3 and g (x) = x^{2} + 7$ , then the values of x such that $g (f (x)) = 8$ are
A1,2
B $- 1, 2$
C $- 1, - 2$
D $1, - 2$