In a right-angled isosceles triangle, the measures of the angles are _______.
The correct Answer is:45∘,45∘,90∘
To find the measures of the angles in a right-angled isosceles triangle, we can follow these steps:
1. Understand the Properties of the Triangle:
A right-angled isosceles triangle has one angle that is a right angle (90 degrees) and the other two angles are equal.
Hint: Remember that in an isosceles triangle, two angles are always the same.
2. Identify the Right Angle:
In this triangle, we know that one angle is 90 degrees. Let's denote the angles as A, B, and C. We can say that angle B = 90 degrees.
Hint: A right-angled triangle has one angle that measures exactly 90 degrees.
3. Use the Angle Sum Property:
The sum of all angles in any triangle is 180 degrees. Therefore, we can write the equation:
A+B+C=180
Substituting the known value of angle B:
A+90+C=180
Hint: The total measure of angles in any triangle is always 180 degrees.
4. Simplify the Equation:
Rearranging the equation gives us:
A+C=180−90
A+C=90
Hint: After finding one angle, subtract it from 180 to find the sum of the other two angles.
5. Determine the Equal Angles:
Since angles A and C are equal (because it is an isosceles triangle), we can say:
A=C
Therefore, we can write:
A+A=90
or
2A=90
Hint: If two angles are equal, you can combine them into one expression.
6. Solve for Angle A:
Dividing both sides by 2 gives:
A=902=45
Hint: To find the measure of one angle, divide the total by the number of equal angles.
7. Find Angle C:
Since angle C is equal to angle A, we have:
C=45
Hint: In an isosceles triangle, the two equal angles will have the same measure.
8. Conclusion:
The measures of the angles in a right-angled isosceles triangle are:
- Angle A = 45 degrees
- Angle B = 90 degrees
- Angle C = 45 degrees
Therefore, the final answer is:
The measures of the angles are 45 degrees, 90 degrees, and 45 degrees.
A right-angled isosceles triangle has one angle that is a right angle (90 degrees) and the other two angles are equal.
In this triangle, we know that one angle is 90 degrees. Let's denote the angles as A, B, and C. We can say that angle B = 90 degrees.
The sum of all angles in any triangle is 180 degrees. Therefore, we can write the equation:
A+B+C=180
Substituting the known value of angle B:
A+90+C=180
Rearranging the equation gives us:
A+C=180−90
A+C=90
Since angles A and C are equal (because it is an isosceles triangle), we can say:
A=C
Therefore, we can write:
A+A=90
or
2A=90
Dividing both sides by 2 gives:
A=902=45
Since angle C is equal to angle A, we have:
C=45
The measures of the angles in a right-angled isosceles triangle are:
- Angle A = 45 degrees
- Angle B = 90 degrees
- Angle C = 45 degrees
The measures of the angles are 45 degrees, 90 degrees, and 45 degrees.
Topper's Solved these Questions
- GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRYExercise:SHORT ANSWER TYPE QUESTIONS
Explore 19 Videos
- GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRYExercise:CONCEPT APPLICATION
Explore 5 Videos
- GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRYExercise:CROSSWORD
Explore 1 Video
- FRACTIONS AND DECIMALS Book:PEARSON IIT JEE FOUNDATIONChapter:FRACTIONS AND DECIMALS Exercise:Crossword
Explore 1 Video
- MENUSRATION Book:PEARSON IIT JEE FOUNDATIONChapter:MENUSRATION Exercise:Crossword
Explore 1 Video
Similar Questions
Knowledge Check
In a right-angled isosceles triangle, the ratio of the circumradius and inradius is
A2(√2+1):1B(√2+1):1C2:1D√2:1In a right - angled isosceles triangle , the ratio of the circumradius and inradius is
A2(√2+1):1B(sqrT(2)+1):1C2:1D√2:1The hypotenuse of a right-angled isosceles triangle is 5 cm. The area of the triangle is (a) 5 cm2 (b) 6.25 cm2 (c) 6.5 cm2 (d) 12.5 cm2
A5 cm2B6.25 cm2C6.5 cm2D12.5 cm2
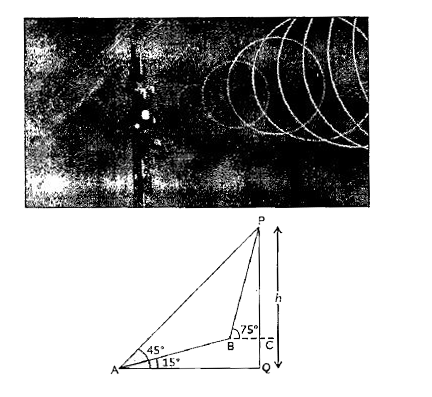
In right angled triangle APQ, BC∣∣AQ, the measure if ∠BPC is
View SolutionIn a right-angled triangle if an angle measures 35°, then find the measure of the third angle.
View SolutionThe vertex angle of an isosceles triangle is 80∘ , Find ot the measure of base angles .
View SolutionIf the exterior angle of a regular polygon is equal to the acute angle of a right-angled isosceles triangle, then the polygon is a regular
View SolutionA non right angle bisector of a right angled isosceles triangle divide the triangle in those two parts, whose area are in the ratio.
View Solution