The integral form of the exponential growth equation as Nt=N0ert
A. population density after time t
B. population density at time zero
C. intrinsic rate of natural increase
D. the base of natural logarithms (2.71828)
Identify A,B,C and D fromt eh given equation.
A-r,B-e,C-No,D-Nt
A−Nt,B−N0,C−r,D−e
A−N0,B−Nt,C−r,D−e
A−N0,B−Nt,C−e,D−r
The correct Answer is:B
To identify A, B, C, and D from the given exponential growth equation Nt=N0ert, we can break down the equation and analyze each component step by step.
1. Understanding the Equation:
The equation Nt=N0ert represents the exponential growth of a population over time. Here, Nt is the population size at time t, N0 is the initial population size, r is the intrinsic rate of natural increase, and e is the base of natural logarithms.
2. Identifying A:
- Nt represents the population density after time t.
- Therefore, A = Nt.
3. Identifying B:
- N0 represents the population density at time zero (the initial population size).
- Therefore, B = N0.
4. Identifying C:
- The intrinsic rate of natural increase is represented by r in the equation.
- Therefore, C = r.
5. Identifying D:
- The base of natural logarithms is denoted by e, which is approximately 2.71828.
- Therefore, D = e.
Summary of Identifications:
- A = Nt (population density after time t)
- B = N0 (population density at time zero)
- C = r (intrinsic rate of natural increase)
- D = e (the base of natural logarithms)
Conclusion:
Based on the identifications, the correct option is the second one, which states:
- A is Nt
- B is N0
- C is r
- D is e
The equation Nt=N0ert represents the exponential growth of a population over time. Here, Nt is the population size at time t, N0 is the initial population size, r is the intrinsic rate of natural increase, and e is the base of natural logarithms.
- Nt represents the population density after time t.
- Therefore, A = Nt.
- N0 represents the population density at time zero (the initial population size).
- Therefore, B = N0.
- The intrinsic rate of natural increase is represented by r in the equation.
- Therefore, C = r.
- The base of natural logarithms is denoted by e, which is approximately 2.71828.
- Therefore, D = e.
- A = Nt (population density after time t)
- B = N0 (population density at time zero)
- C = r (intrinsic rate of natural increase)
- D = e (the base of natural logarithms)
Based on the identifications, the correct option is the second one, which states:
- A is Nt
- B is N0
- C is r
- D is e
Similar Questions
Draw and explain a logistic curve for a population of density (N) at time (t ) whose intrinsic rate of natural increase is (r) and carrying capacity is (k).
View Solution(a) Write an equation for Verhulst Pearl logistic . Growth where
N = Population density at a time t
r = Intrinsic rate of natural increase
K = Carrying capacity
(b) Draw a graph for a population whose population density has reached the carrying capacity .
(c) Why is the logistic growth model considered a more reallistic one for most animal populations ?
(d) Draw a growth curve where resources are not limiting to growth of a population.
View Solution
Knowledge Check
dN/dt=rN(K−NK)
A-population at time t
B-Intrinsic rate of natural increase
C-carrying capacity
Identify A,B, and C from given equationAABCNKrBABCNrKCABCKNrDABCKrNIf N= population density at time t, then population density at time t+1 can be written as. Nt+1=Nt+[(A+B)−(C+D)]. Select the correct option for A,B,C and D in the above equation.
AA can be mortality and B can be natalityBB can be immigration and C can be natalityCC can be mortality and D can be immigrationDA can be natality and D can be emigration.Population A-have the intrinsic rate of natural incease in 0.2
Population B-have the intrinsic rate of natural increase is 0.3
Population C-have the intrinsic rate of natural increases is 0.4
Population D-have the intrinsic rate of natural increase is 0.5
Which population will increase fastest among all of the given population ?ADBCCBDA
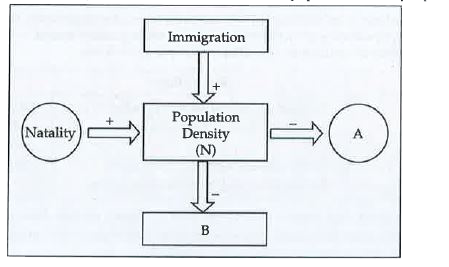
Observe flow chart given below:
(a) Name the processes represented as A and B.
(b) If 'N' , is the population density at time t, then write down the population density equation at time t+1.
View SolutionTwo identical capacitor A and B, charged to the same potential 5V are connected in two different circuits as shown below at time t=0. t=CR is QAandQB respectively, then (Here e is the base of natureal logarithm)

View SolutionA⊕−−→ population density(N)T←−−B.
If A increases the population density and B decrases then identify A and B
View SolutionIf natality is represented by -B
If mortality is represented by -D
if immigration is represented -I
If emigration is represented by -E
If population density at time t+1 is represented by
View SolutionThe given figure represents different factors affecting population density (N). If B= natality D= mortality ,E=emigration and I= immigration, then select the incorrect option regarding these.

View Solution
