(a) Write an equation for Verhulst Pearl logistic . Growth where
N = Population density at a time t
r = Intrinsic rate of natural increase
K = Carrying capacity
(b) Draw a graph for a population whose population density has reached the carrying capacity .
(c) Why is the logistic growth model considered a more reallistic one for most animal populations ?
(d) Draw a growth curve where resources are not limiting to growth of a population.
Video Solution
Text Solution
(a) Density equation = dNdt=rN(K−NK)
(b and d )
(a) When responses are not limiting the growth .
(b) When responses are limiting the growth . K = Carrying capacity .
(c) The resources for growth for most animal populations are finite and become limiting sooner or later . This is why the logistic growth model is considered a more realistic one.
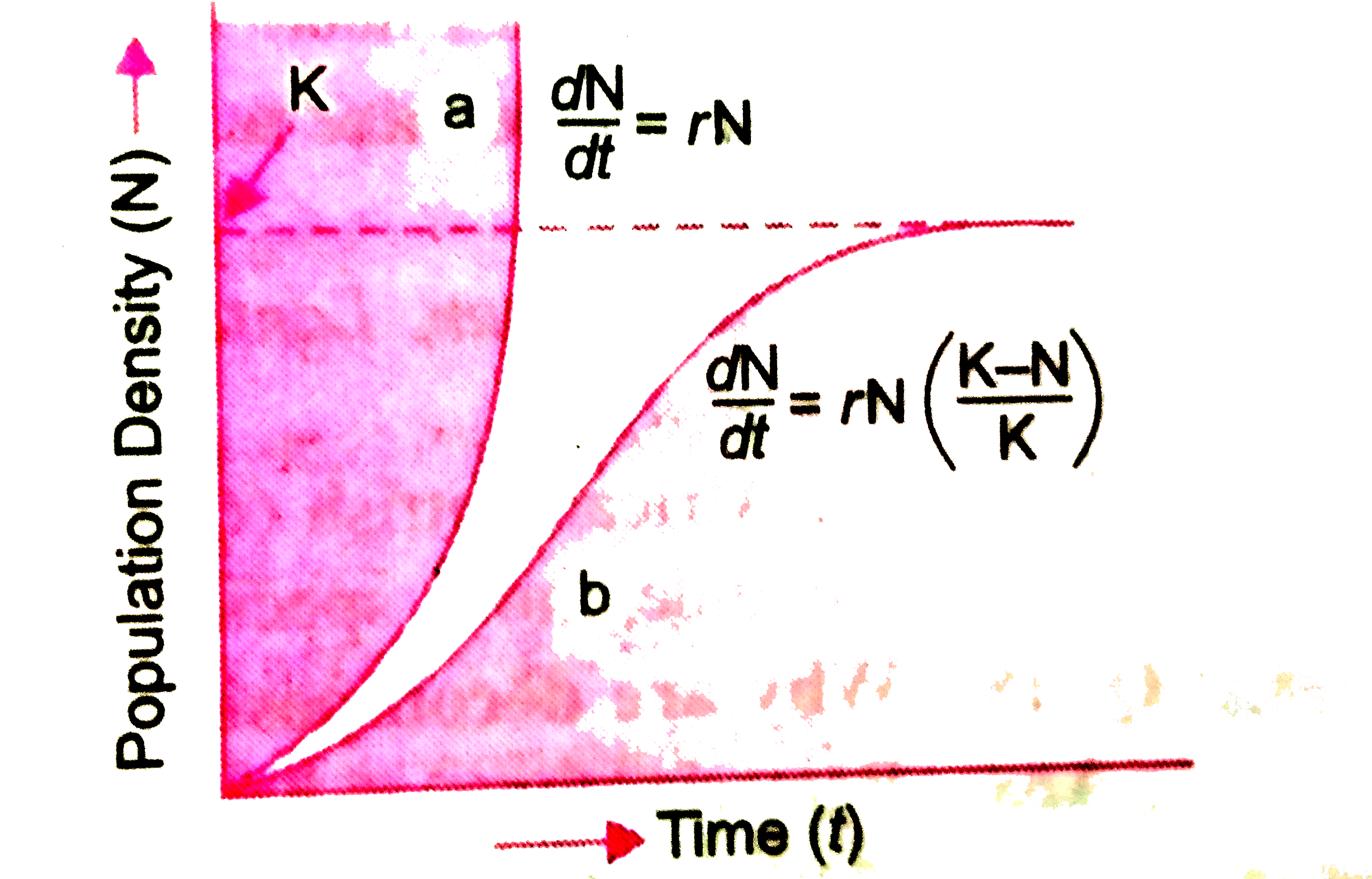
|
Topper's Solved these Questions
- ORGANISMS AND POPULATIONS BOOK - PRADEEPCHAPTER - ORGANISMS AND POPULATIONS EXERCISE - Practice Questions (I. Multiple Choice Questions)
87 Videos
- ORGANISMS AND POPULATIONS BOOK - PRADEEPCHAPTER - ORGANISMS AND POPULATIONS EXERCISE - Practice Questions (II. Assertion - Reason Type Questions)
18 Videos
- ORGANISMS AND POPULATIONS BOOK - PRADEEPCHAPTER - ORGANISMS AND POPULATIONS EXERCISE - Long Answer Questions
29 Videos
- ORGANISMS AND POPULATIONORGANISMS AND POPULATIONSBOOK - PRADEEPCHAPTER - ORGANISMS AND POPULATIONORGANISMS AND POPULATIONSEXERCISE - Additional Questions (Very Short Answer Questions)
1 Videos
- PRINCIPLES OF INHERITANCE AND VARIATION BOOK - PRADEEPCHAPTER - PRINCIPLES OF INHERITANCE AND VARIATION EXERCISE - ASSERTION-REASON TYPE QUESTIONS
15 Videos
Similar Questions
Knowledge Check
Verhulst-pearl logistic growth patten is
ASigmoidBJ-shapedCStraight lineDHyperbolaVerhulst-pearl logistic growth patten is
AsigmoidBj-shapedCstraight lineDhyperbolaA population that has not reached the carrying capacity is likely to :
Adecline in numberBgrow exponentiallyCremain stable in numberDgrow but not at an exponential rate
Draw and explain a logistic curve for a population of density (N) at time (t ) whose intrinsic rate of natural increase is (r) and carrying capacity is (k).
View SolutionA population that not has to reached the carrying capacity is likely to :
View SolutionVerhult - Pearl logistic growth pattern is :-
View SolutionVerhulst - Pearl Logistic growth equation is :
View SolutionWhen population reaches carrying capacity :
View Solution
