The energy of activation for a reaction is 50kJ/ mol. Presence of a catalyst lowers the energy of activation by 25%. What will be the effect on rate of reaction at C- Other things remains same.
142.75
242.75
342.75
442.75
The correct Answer is:A
To solve the problem, we need to determine the effect of a catalyst on the rate of reaction by calculating the change in the rate constant due to the decrease in activation energy.
1. Identify the given values:
- Activation energy (Ea) = 50 kJ/mol
- Decrease in activation energy due to catalyst = 25%
- Temperature (T) = 30°C = 303 K (after converting to Kelvin)
2. Calculate the new activation energy (Ea') after the catalyst is added:
- Decrease in Ea = 25% of 50 kJ/mol
- Decrease in Ea = (25/100) * 50 kJ/mol = 12.5 kJ/mol
- New activation energy (Ea') = 50 kJ/mol - 12.5 kJ/mol = 37.5 kJ/mol
3. Convert activation energies from kJ/mol to J/mol for calculations:
- Ea = 50 kJ/mol = 50,000 J/mol
- Ea' = 37.5 kJ/mol = 37,500 J/mol
4. Use the Arrhenius equation to find the rate constants (k1 and k2):
- The Arrhenius equation is given by:
k=Ae−EaRT
- For the original activation energy (k1):
k1=Ae−50,000RT
- For the new activation energy (k2):
k2=Ae−37,500RT
5. Calculate the ratio of the rate constants (k2/k1):
- Dividing the two equations:
k2k1=Ae−37,500RTAe−50,000RT
- This simplifies to:
k2k1=e−37,500−50,000RT=e−−12,500RT=e12,500RT
6. Substitute R (8.314 J/mol·K) and T (303 K) into the equation:
- Calculate:
12,500R⋅T=12,5008.314⋅303
- Calculate the value:
12,5008.314⋅303≈0.5
- Therefore:
k2k1=e0.5≈1.6487
7. Interpret the result:
- The rate of reaction increases by a factor of approximately 1.6487 due to the presence of the catalyst.
Conclusion:
The presence of a catalyst increases the rate of reaction by approximately 1.6487 times at 30°C.
- Activation energy (Ea) = 50 kJ/mol
- Decrease in activation energy due to catalyst = 25%
- Temperature (T) = 30°C = 303 K (after converting to Kelvin)
- Decrease in Ea = 25% of 50 kJ/mol
- Decrease in Ea = (25/100) * 50 kJ/mol = 12.5 kJ/mol
- New activation energy (Ea') = 50 kJ/mol - 12.5 kJ/mol = 37.5 kJ/mol
- Ea = 50 kJ/mol = 50,000 J/mol
- Ea' = 37.5 kJ/mol = 37,500 J/mol
- The Arrhenius equation is given by:
k=Ae−EaRT
- For the original activation energy (k1):
k1=Ae−50,000RT
- For the new activation energy (k2):
k2=Ae−37,500RT
- Dividing the two equations:
k2k1=Ae−37,500RTAe−50,000RT
- This simplifies to:
k2k1=e−37,500−50,000RT=e−−12,500RT=e12,500RT
- Calculate:
12,500R⋅T=12,5008.314⋅303
- Calculate the value:
12,5008.314⋅303≈0.5
- Therefore:
k2k1=e0.5≈1.6487
- The rate of reaction increases by a factor of approximately 1.6487 due to the presence of the catalyst.
The presence of a catalyst increases the rate of reaction by approximately 1.6487 times at 30°C.
Topper's Solved these Questions
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -2 (H.W) (ORDER OF REACTION)
Explore 16 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -2 (H.W) (HALF LIFE)
Explore 13 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -2 (C.W) COLLISION THEORY
Explore 2 Videos
- CARBOXYLIC ACIDBook:NARAYNAChapter:CARBOXYLIC ACIDExercise:All Questions
Explore 288 Videos
- CHEMISTRY IN EVERYDAY LIFEBook:NARAYNAChapter:CHEMISTRY IN EVERYDAY LIFEExercise:ASSERTION & REASON TYPE QUESTIONS
Explore 10 Videos
Similar Questions
Rate expression for Xa+Yb→ products is Rate =K[A]m[B]n. Units of K w.r.t A and B respectively are s−1 and M−1s−1, when concentrations of A and B are increased by 4 times, then
View SolutionThe half life for the reaction N2O5⇔2NO2+12O2 in 24hr at 30∘C. Starting with 10g of N2O5 how many grams of N2O5 will remain after a period of 96 hours ?
View SolutionFor A+B→C+D,ΔH=−20kJmole−1. The activation energy for the forward reaction is 85 kJ. Then the activation energy for the backward reaction is ___
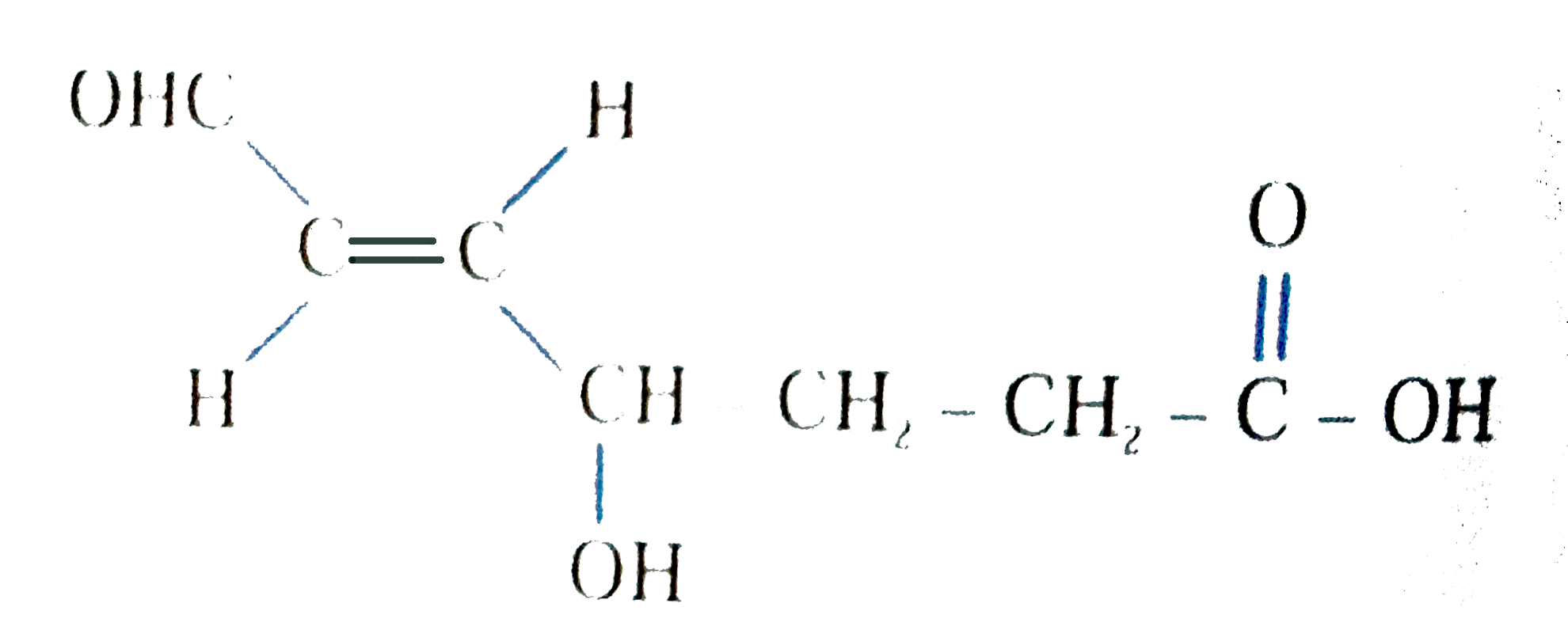
View SolutionProvide IUPAC name of the compound given below.
View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.
View SolutionThe activation energy of a first order reaction at 300K is kJmol−1. In the presence of a catalyst, the activation energy gets lowered to 50kJmol−1 at 300K. How many times the reaction rate change in the presence of a catalyst at the same temperature ?
View SolutionThe energy of activation for a reaction is 100 KJ mol^(-1) . The peresence of a catalyst lowers the energy of activation by 75% . What will be the effect on the rate of reaction at 20^(@)C , other things being equal?
View SolutionAssertion (A) The enthalpy of reaction remains constant in the presence of a catalyst.
Reason (R) A catalyst participating in the reaction froms different activated complex and lowers down the activation energy but the difference in energy of reactant and product remains the same.
View SolutionThe activation energy of a first order reaction at 300 K is 60 kJ "mol"^(-1) . In the presence of a catalyst, the activation energy is lowered to 50 kJ "mol"^(-1) at the same teperature. How many times the rate of reaction will change ?
View SolutionAssertion (A) The enthalpy of reaction remains constant in the presence of a catalyst.
Reason (R) A catalyst participating in the reaction froms different activated complex and lowers down the activation energy but the difference in energy of reactant and product remains the same.
View SolutionThe activation energy of a reaction is 100 kJ/mol. In the presence of catalyst the activation energy is decreased by 75%. What is the effect on rate constant of the reaction at 20^@ C ?
View SolutionA hydrogenation reaction is carried out at 500K. If the same reaction is carried out in presence of catalyst at the same rate, the temperature required is 400K. Calculate the activation energy of the reaction if the catalyst lowers the activation energy barrier by 20kJ/mol.
View SolutionThe energy of activation for a reaction is 100kJ//mol . Presence of catalyst lowers the energy of activation by 75% . What will be effect on rate of reaction at 20^(@)C , other things being equal ?
View SolutionWith 100 kJ mol- activation energy for an uncatalysed reaction at 20°C, the catalyst lowers the energy of activation by 75%. What will be the effective rate if other conditions are same?
View SolutionThe energy of activation for a reaction is 100 kJ/mol at 57^(@)C . Presence of catalyst lower activation energy by 25%. The rate of reaction is increased by 10^(x) the value of x is
View Solution