For the reaction,
N2O5→2NO2+O2,Given
−d[N2O5]dt=K1[NO2O5]
d[NO2]dt=K2[N2O5]andd[O2]dt=K3[N2O5]
The relation in between K1,K2 and K3 is:
K1=2K2=3K3
2K1=4K2=K3
2K1=K2=4K3
K1=K2=K3
The correct Answer is:C
2×−ddt[N2O5]=ddt[NO2]=4d[O2]ddt
1.0M→0.6M(40%)
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -2 (C.W) HALF LIFE
4 Videos
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -2 (C.W) COLLISION THEORY
2 Videos
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -2 (C.W) RATE OF REACTION & FACTORS
31 Videos
- CARBOXYLIC ACIDBOOK - NARAYNACHAPTER - CARBOXYLIC ACIDEXERCISE - All Questions
288 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - NARAYNACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - ASSERTION & REASON TYPE QUESTIONS
10 Videos
Similar Questions
The half life period of a first order reaction is 10 minutes . The time required for the concentration of the reactant to change from 0.08 M to 0.02is :
View SolutionFor A+B→C+D,ΔH=−20kJmole−1. The activation energy for the forward reaction is 85 kJ. Then the activation energy for the backward reaction is ___
View SolutionFor the elem entary reaction 2A→C the concentration of A after 30 minutes was found to be 0.01 mole/lit. If the rate constant of the reaction is 2.5×10−2 lit mole−1sec−1 the rate of the reaction at 30 minutes is
View SolutionProvide IUPAC name of the compound given below.
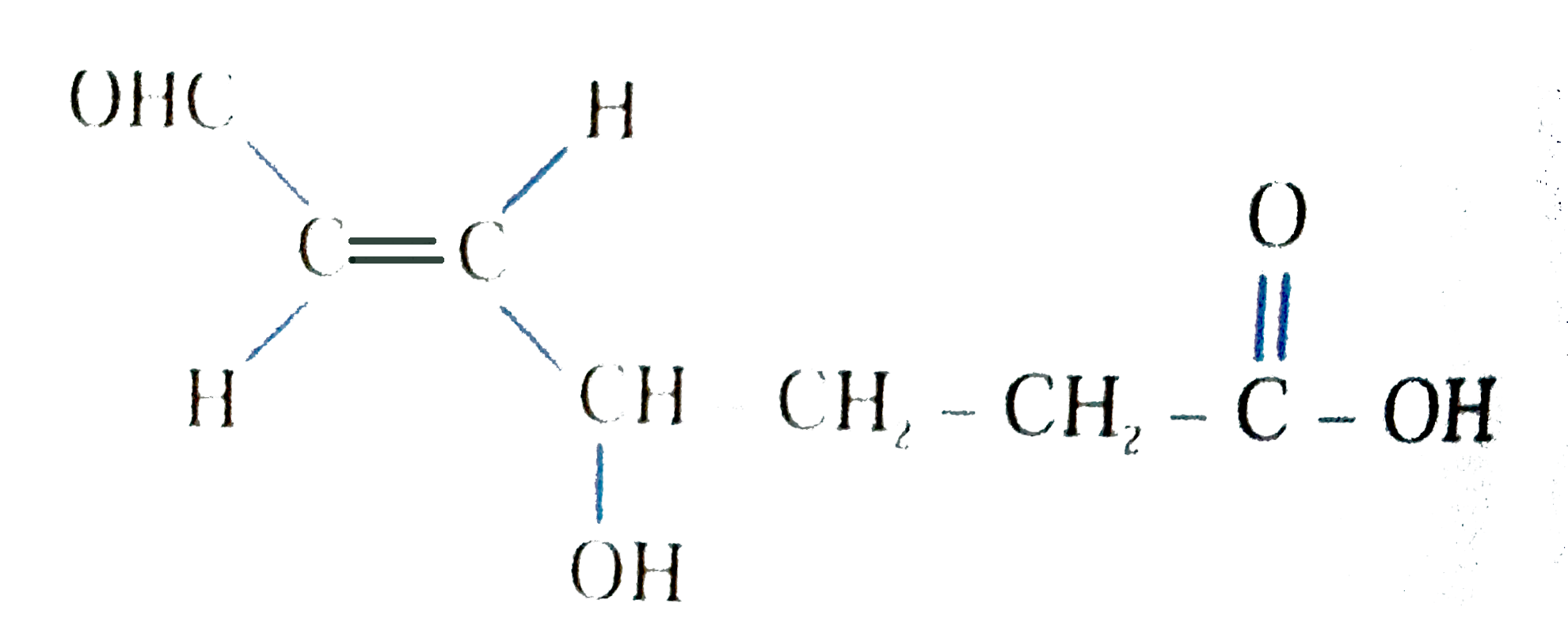
View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.
View SolutionWhen N_(2)O_(5)(g) is heated it dissociates to give N_(2)O_(3) and O_(2) . K_(c) for N_(2)O_(5)rarr N_(2)O_(3)+O_(2) is 7.75 and K_(c) for N_(2)O_(3)rarr N_(2)O+O_(2) is 4.0 mol L^(-1) . (both K_(c) are at same temperature) 4 mol N_(2)O_(5) in 1.0L vessel is kept at a certain temperature. the concentration of O_(2) was 4.5 mol L^(-1) . Find the concentration of N_(2)O_(5), N_(2)O_(3) , and N_(2)O at equilibrium.
View Solution2N2O5→4NO2+O2
If −d[N2O5]dt=k1[N2O5]
d[NO2]dt=k2[N2O5]
d[O2]dt=k3[N2O5]
What is the relation between k1,k2, and k3?
View SolutionFor the reaction,
N2O5→2NO2+12O2,Given
−d[N2O5]dt=K1[NO2O5]
d[NO2]dt=K2[N2O5]andd[O2]dt=K3[N2O5]
The relation in between K1,K2 and K3 is:
View SolutionConsider the following reaction, 2N_(2)O_(5)rarr4NO_(2)+O_(2),(d[NO_(2)] )/(dt)=k_(2)[N_(2)O_(5)] , (d[O_(2)])/(dt)=k_(3)[N_(2)O_(5)]" and "(d)/(dt)[N_(2)O_(5)]=k_(1) The relation between k_(1), k_(2) and k_(3) is
View SolutionConsider the decomposition of N2O5 as
N2O5→2NO2+1/2O2
The rate of reaction is given by
−d[N2O5]dt=12d[NO2]dt=2d[O2]dt
=k1[N2O5]
Therefore −d[N2O5]dt=k1[N2O5]
+d[NO2]dt=2k1[N2O5]=k1[N2O5]
+d[O2]dt=12k1[N2O5]=k1[N2O5]
Choose the correct option
View SolutionConsider the decomposition of N2O5 as
N2O5→2NO2+1/2O2
The rate of reaction is given by
−d[N2O5]dt=12d[NO2]dt=2d[O2]dt
=k1[N2O5]
Therefore −d[N2O5]dt=k1[N2O5]
+d[NO2]dt=2k1[N2O5]=k1[N2O5]
+d[O2]dt=12k1[N2O5]=k1[N2O5]
Choose the correct option
View SolutionThe thermal decomposition of N_(2)O_(5) occues as: 2N_(2)O_(5) rarr 4NO_(2)+O_(2) Experimental studies suggest that rate of decomposition of N_(2)O_(5) rate of formation of NO_(2) or rate of formation of O_(2) all becomes double if concentration of N_(2)O_(5) is doubled. If rate constants for decomposition of N_(2)O_(5) formation of NO_(2) and O_(2) are k_(1),k_(2) and k_(3) respectively, then:
View Solution2N_(2)O_(5)rarr NO_(2)+O_(2), (d[N_(2)O_(5)])/(dt)=k_(1)[N_(2)O_(5)], (d[NO_(2)])/(dt)=k_(2)[N_(2)O_(5)] and (dO_(2))/(dt)=k_(3)[N_(2)O_(5)] , the relation between k_(1), k_(2) and k_(3) is
View SolutionConsider the reaction 2N2O5(g)→4NO2(g)+O2(g) whose rate can be expressed any one of the following expressions (1)−d[N2O5]dt=k1[N2O5] or (2)d[NO2]dt=k2[N2O5] or (3)d[O2]dt=k3[N2O5]
Find the relation between k1,k2andk3 .
View Solution2N2O5→4NO2+O2,d[N2O5]dt=k1[N2O5].
d[NO2]dt=k2[N2O5]andd[O2]dt=k3[N2O5], the relation between k1,k2andk3 is
View Solution2N2O5→4NO2+O2,d[N2O5]dt=k1[N2O5].
d[NO2]dt=k2[N2O5]andd[O2]dt=k3[N2O5], the relation between k1,k2andk3 is
View Solution
