For a first order reaction, is 1386 seconds, then the specific rate constant in is
The correct Answer is:A
To find the specific rate constant k for a first-order reaction given that t0.75=1386 seconds, we can follow these steps:
1. Understand t0.75:
- The term t0.75 refers to the time taken for 75% of the reactant to be converted into products. This means that 25% of the reactant remains.
2. Set up the relationship:
- For a first-order reaction, the relationship between t0.75 and the rate constant k is given by the formula:
t0.75=2.303klog((A0)(A))
- Here, (A0) is the initial concentration and (A) is the concentration at time t0.75.
3. Determine concentrations:
- If we assume the initial concentration (A0)=100 (arbitrary units), then after 75% of the reaction, the remaining concentration (A) will be:
(A)=100−75=25
- Thus, the ratio (A0)(A) becomes:
10025=4
4. Substitute values into the formula:
- Now, substituting the values into the equation:
1386=2.303klog(4)
5. Calculate log(4):
- We know that log(4)=2log(2). Using log(2)≈0.301:
log(4)≈2×0.301=0.602
6. Rearranging the equation:
- Now, we can rearrange the equation to solve for k:
k=2.303⋅log(4)1386
- Substituting log(4):
k=2.303⋅0.6021386
7. Calculate k:
- Performing the multiplication:
k≈1.3841386≈0.000999sec−1
- This can be approximated to k≈10−3sec−1.
Final Answer:
The specific rate constant k is approximately 10−3sec−1.
- The term t0.75 refers to the time taken for 75% of the reactant to be converted into products. This means that 25% of the reactant remains.
- For a first-order reaction, the relationship between t0.75 and the rate constant k is given by the formula:
t0.75=2.303klog((A0)(A))
- Here, (A0) is the initial concentration and (A) is the concentration at time t0.75.
- If we assume the initial concentration (A0)=100 (arbitrary units), then after 75% of the reaction, the remaining concentration (A) will be:
(A)=100−75=25
- Thus, the ratio (A0)(A) becomes:
10025=4
- Now, substituting the values into the equation:
1386=2.303klog(4)
- We know that log(4)=2log(2). Using log(2)≈0.301:
log(4)≈2×0.301=0.602
- Now, we can rearrange the equation to solve for k:
k=2.303⋅log(4)1386
- Substituting log(4):
k=2.303⋅0.6021386
- Performing the multiplication:
k≈1.3841386≈0.000999sec−1
- This can be approximated to k≈10−3sec−1.
The specific rate constant k is approximately 10−3sec−1.
Topper's Solved these Questions
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -2 (C.W) HALF LIFE
Explore 4 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -2 (C.W) COLLISION THEORY
Explore 2 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -2 (C.W) RATE OF REACTION & FACTORS
Explore 31 Videos
- CARBOXYLIC ACIDBook:NARAYNAChapter:CARBOXYLIC ACIDExercise:All Questions
Explore 288 Videos
- CHEMISTRY IN EVERYDAY LIFEBook:NARAYNAChapter:CHEMISTRY IN EVERYDAY LIFEExercise:ASSERTION & REASON TYPE QUESTIONS
Explore 10 Videos
Similar Questions
The half life period of a first order reaction is 10 minutes . The time required for the concentration of the reactant to change from 0.08 M to 0.02is :
View SolutionFor A+B→C+D,ΔH=−20kJmole−1. The activation energy for the forward reaction is 85 kJ. Then the activation energy for the backward reaction is ___
View SolutionFor the elem entary reaction 2A→C the concentration of A after 30 minutes was found to be 0.01 mole/lit. If the rate constant of the reaction is 2.5×10−2 lit mole−1sec−1 the rate of the reaction at 30 minutes is
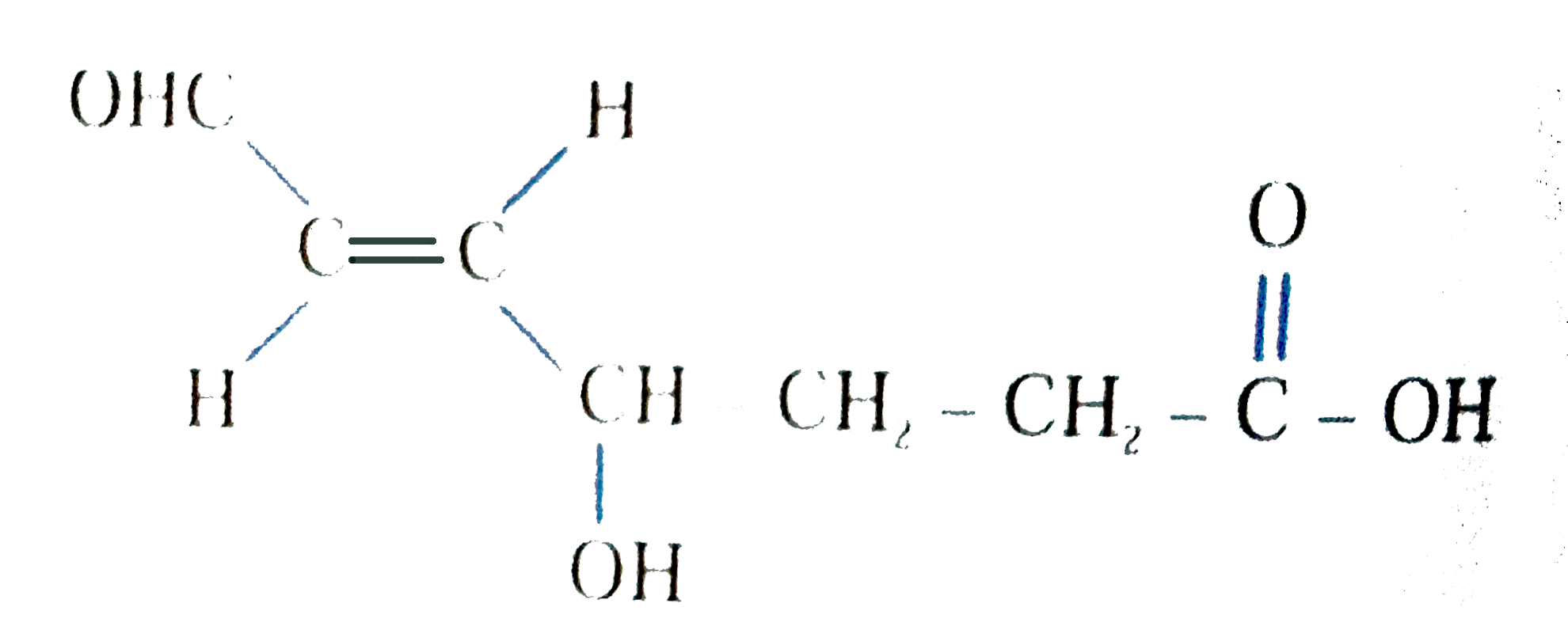
View SolutionProvide IUPAC name of the compound given below.
View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.
View SolutionFor a first order reaction t0.75 is 1386s. Therefore, the specific rate constant is
View SolutionThe specific rate constant of a first order reaction depends on the
View SolutionHalf-life period of a first-order reaction is 1386 seconds. The specific rate constant of the reaction is
View SolutionHalf life period of a first-order reaction is 1386 seconds . The specific rate constant of the reaction is
View SolutionThe specific rate constant of a first order reaction depends on the
View Solutionकिसी प्रथम कोटि की अभिक्रिया का अर्द्ध-आयु काल 1386 सेकण्ड है उस अभिक्रिया का विशिष्ट दर स्थिरांक है
View SolutionFor a first order reaction t0.75 is 1368 seconds, therefore, the specific rate constant in sec−1 is
View SolutionHalf the period of a first order reaction is 1386 seconds . The specific rate constant of the reaction is :
View SolutionFor a first reaction, t_(0.75) is 138.6 seconds. Its specific rate constant (in sec^(-1) ) is
View SolutionFor first order reaction t_(0.75) is 138.6 sec. Its specific rate constant is (in s^(-1) )
View Solution

