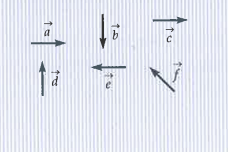
Six vector →a through →f have the magnitudes and direction indicated in the figure. Which of the following statements is true?
→b+→e=→f
→b+→c=→f
→d+→c=→f
→d+→e=→f
The correct Answer is:4
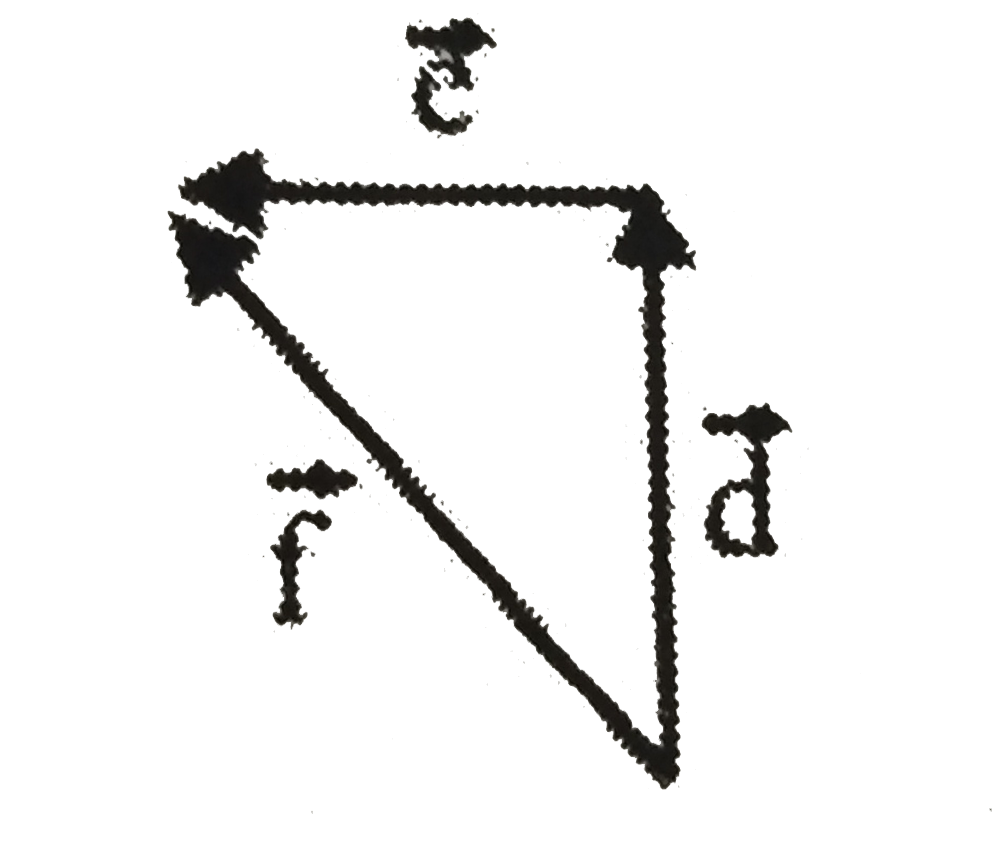
⇒→f=→d+→e
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-III CHECK YOUR UNDERSTANDING15videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - CROSS PRODUCT15videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
Similar Questions
Knowledge Check
- Question 1 - Select One
Six vectors ˆa to ˆi have the magnitude and directions indicated in the figure . Which of the following statement is true ?
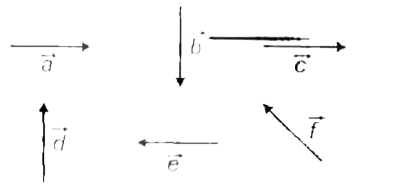 A→b+→e=→fB→b+→c=→fC→d+→c=→fD→d+→e=→f
A→b+→e=→fB→b+→c=→fC→d+→c=→fD→d+→e=→f - Question 2 - Select One
If →P×→Q=→R, then which of the following statements is not true?
A→R⊥→PB→R⊥→QC→R⊥(→P+→Q)D→R⊥(→P×→Q) - Question 3 - Select One
If →A,→B,→C are mutually perpendicular vectors then which of the following statements is wrong?
A→C×(→A×→B)=0B→A×→B∣∣→A×→B∣∣=→C∣∣→C∣∣C→A.→B=→B.→C=→C.→A=0D(→B+→C) is perpendicular to →A
Consider the following statements:
1. The magnitude of →a×→b is same as the area of a triangle with sides →aand→b.
2. If →a×→b=→0 where →a≠0.→b≠0 then →a=λ→b which of the following statements is/are correct?View SolutionTwo vector →A and →B have equal magnitudes. Then the vector →A+→B is perpendicular :
View SolutionThe angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
View SolutionThree coplanar vectrors →A,→B and →C have magnitudes 4,3 and 2 respectively. If the angle any two vector is 120∘ then which of the following vector may be equal to 3→A4+→B3+→C2
 View Solution
View Solution→A is a vector with magnitude A, then the unit vector ˆA in the direction →A is
View Solution