The angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
A
A=2B
B
A=B/2
C
A=B
D
AB=1
Video Solution
Text Solution
The correct Answer is:C
Graphically:
∠ROQ=θ/2,∠RQO=θ/2
Hence, ΔOQR is isosceles.
⇒OR=RQ⇒B=A
Analytically:
tan(θ/2)=BsinθA+Bcosθ
⇒sin(θ/2)cos(θ/2)=2Bsin(θ/2)cos(θ/2)A+B[2cos2(θ/2)−1] ltbr ⇒A+2Bcos2(θ/2)−B=2Bcos2(θ/2)⇒A=B
⇒A+2Bcos2(θ/2)−B=2Bcos2(θ/2)⇒A=B
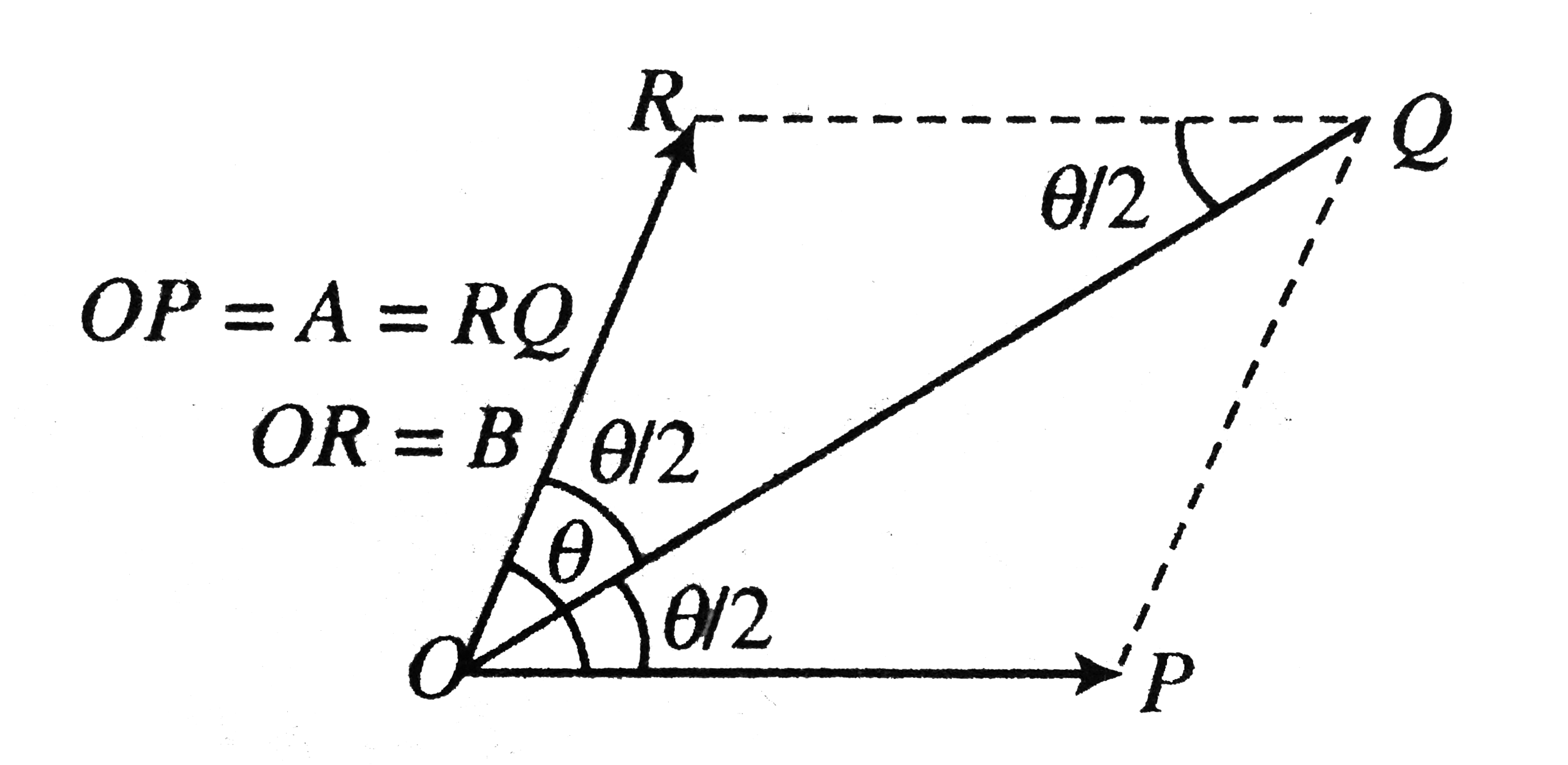
|
Topper's Solved these Questions
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Subjective
Explore 28 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
Similar Questions
Knowledge Check
The angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
AA=2BBA=B/2CA=BDAB=1Let the angle between two nonzero vector →Aand→B is 120∘ and its resultant be →C.
AC=|A−B|BC<|A−B|CC>|A−B|DC=|A+B|Angular between two vectors →Aand→B is θ . Resulatnt of the two makes an angle θ/2 with the vector →A. Select the correct option .
AA=1/BBA=2BCA=BDNone of these
Angle Between Two Vectors
View Solutionif θ angle between two vectors 2i+j+7k and i+5j+k then cosθ
View SolutionIf two vectors →A and →B are at an angle θ≠0∘, then
View Solutionθ is the angle between two vectors a and b then a.b≤0 only if
View SolutionIf the angle between the vectors A and B is θ, the value of the product(BxA)). A is equal to
View Solution

