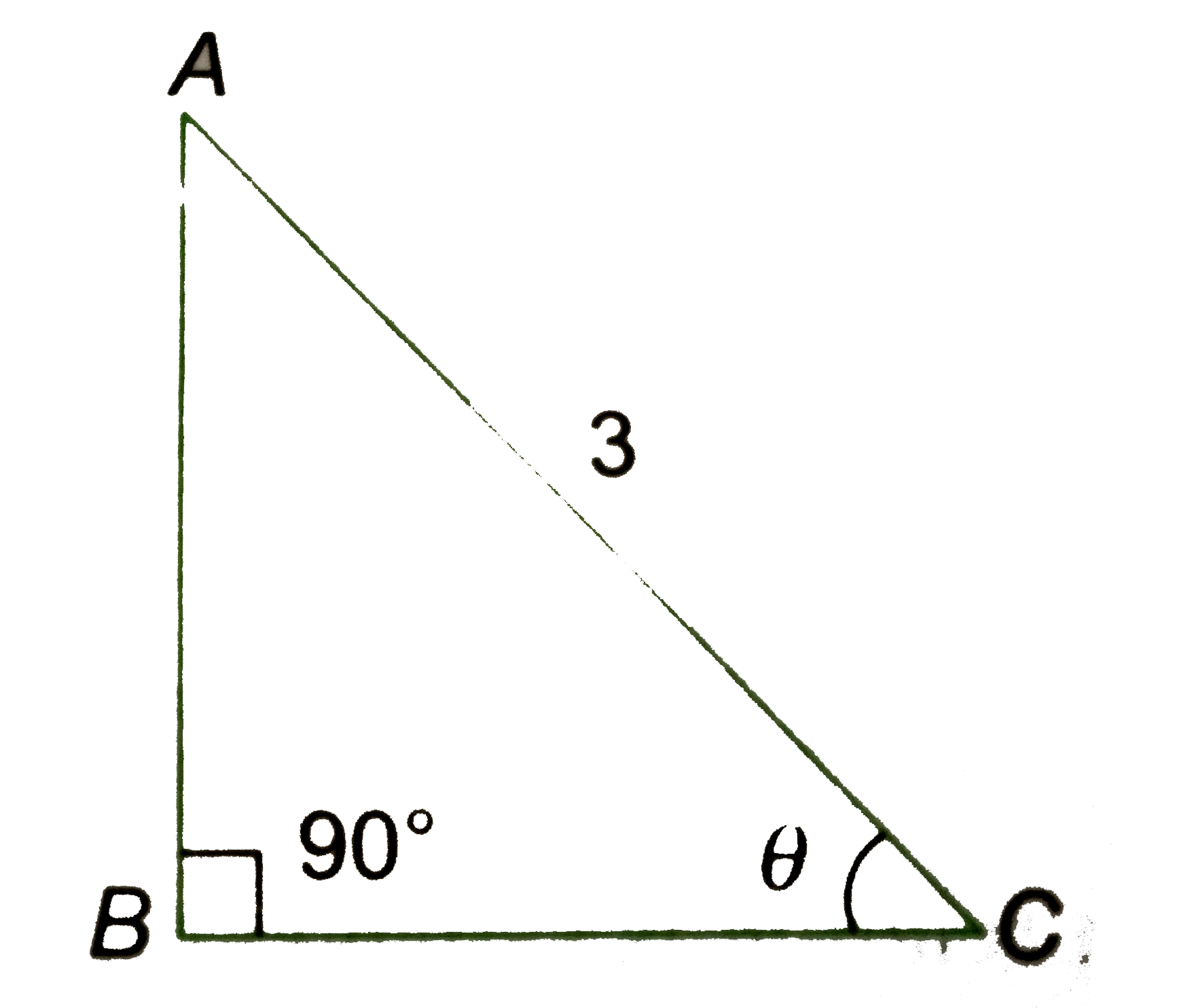
A right triangle has perimeter of length 7 and hypotenuse of length $3 .$ If $θ$ is the larger non-right angle in the triangle, then the value of $cos θ e q u a l .$ $\frac{\sqrt{6} - \sqrt{2}}{4}$ (b) $\frac{4 + \sqrt{2}}{6}$ $\frac{4 - \sqrt{2}}{3}$ (d) $\frac{4 - \sqrt{2}}{6}$

$\frac{\sqrt{6} - \sqrt{2}}{4}$

$\frac{4 + \sqrt{2}}{6}$

$\frac{4 - \sqrt{2}}{3}$

$\frac{4 - \sqrt{2}}{6}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

What is the area of a right angled isosceles triangle whose hypotenuse is $6 \sqrt{2}$ cm?
A12 $c m^{2}$
B18 $c m^{2}$
C24 $c m^{2}$
D36 $c m^{2}$
If the perimeter of an isosceles right triangle is $(6 + 3 \sqrt{2}) m$ , then the area of the triangle is $4.5 m^{2}$ (b) $5.4 m^{2}$ (c) $9 m^{2}$ (d) $81 m^{2}$
A $4.5 m^{2}$
B $5.4 m^{2}$
C $9 m^{2}$
D $81 m^{2}$
If the perimeter of a right angled isosceles triangle is $(6 + 3 \sqrt{2})$ m, then the area of the triangle will be
A4.5 $m^{2}$
B5.4 $m^{2}$
C9 $m^{2}$
D81 $m^{2}$