In a triangle ABC, a=7,b=8,c=9,BD is the median and BE the altitude from the vertex B. Match the following lists
a.BD=p.2b.BE=q.7c.ED=r.√45d.AE=s.6
A
abcdprqq
B
abcdrqsp
C
abcdqrps
D
abcdspqr
Video Solution
Text Solution
The correct Answer is:C

In ΔABD, using Cosine Rule
cosA=42+92−BD22×4×9
In ΔABC, Using Cosine Rule
cosA=82+92−722×8×9
⇒BD2=49
⇒BD=7
ΔBCD is isosceles
⇒ED=CD/2=2
BE=√72−22=√45
AE=6
|
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise (Numerical)
Explore 22 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:JEE Main Previous Year
Explore 2 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise (Comprehension)
Explore 34 Videos
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBook:CENGAGEChapter:PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEExercise:Question Bank
Explore 32 Videos
Similar Questions
Knowledge Check
The sides of a triangle ABC are 6 , 7 , 8 and the smallest angle being C then the length of altitude from C is
A72√15B73√15C74√15DnoneIn ΔABC,∠B is a right angle, AC=6 cm, D is the mid point of AC. The length of BD is
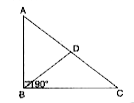 A4 cmB√6 cmC3 cmD3.5 cm
A4 cmB√6 cmC3 cmD3.5 cm
In a triangle ABC, if the median and altitude from A trisect angle A, then (B−C) is (in degrees) equal to……….
View SolutionIn any triangle ABC, the side are a=7,b=5 and c=8. Find A.
View SolutionIn ΔABCif a=7,b=8,c=9 then the distance from the vertex B to the centroid is
View SolutionIn a triangle ABC, ∠B=90∘,AB=8cm,BC=6cm. BD is perpendicular to AC, then find the length of CD, AD and BD.
View SolutionIn a triangle ABC, a, b and c are the lengths of the sides and p, q and r are the lengths of its medians.
Which one of the following is correct ?
View SolutionIn a triangle ABC ,with vertices A(2,3),B(4,−1) and C(1,2) then foot of the altitude which is drawn from the vertex C is
View Solution