A particle when fired at an angle θ=60∘ along the direction of the breadth of a rectangular building of dimension 9m×8m×4m so as to sweep the edges.Find the range of the projectile.
8√3
4√3
8√3
4√3
The correct Answer is:A
m1m2=v2v1,t=(2√v1v2g)
Similar Questions
A short fired at a moving train (u=30 km/h) at an angle θ= arc sin1/5 with the track enters a compartment of dimension a×b=12m×14m through a corner away form the engine and passes out through the diagonally opposite corner. Calculate the speed of the shot.
View SolutionA solid metallic cuboid of dimensions 9m×8m×2 is melted and recast in to solid cubes of edge 2 m .find the number of cubes so formed.
View Solution
Knowledge Check
A cannon fires successively two shells from the same point with velocity V0=250m/s, the first at the angle θ1=60∘ and the second at the angle θ2=45∘ to the horizontal, the azimuth being the same. Neglecting the air drag, find the approximate time interval between firings leading to the collision of the shells (g=9.8m/s2)
A11secB6secC15secD5secA particle is fired from A in the diagonal plane of a building of dimension 20m(length) × 15m (breadth) × 12.5m(height), just clears the roof diagonally & falls on the other side of the building at B.It is observed that the particle is travelling at an angle 45∘ with the horizontal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
The range that is AB will be:
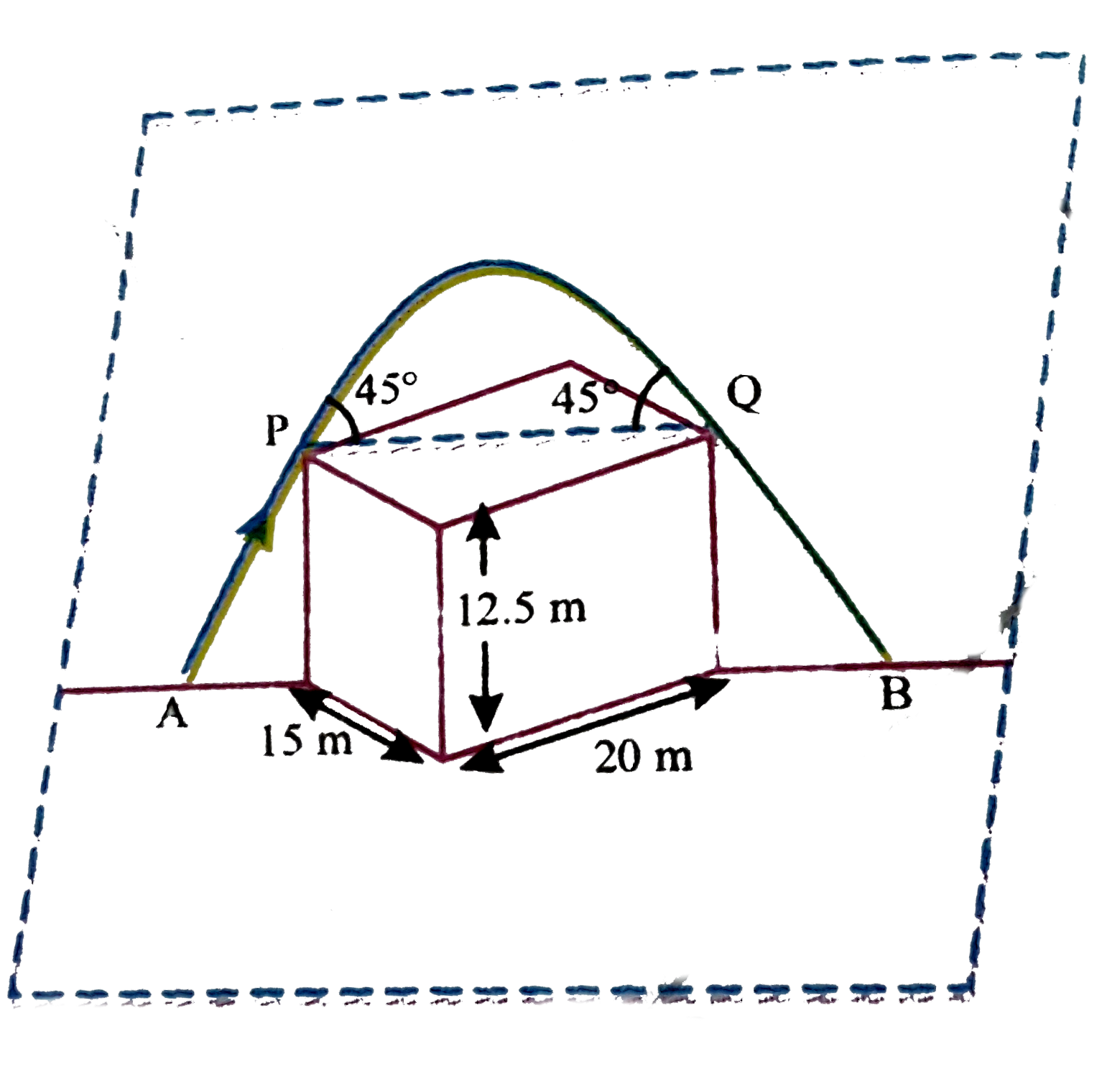 A5√10mB25√3mC5√15mD25√5m
A5√10mB25√3mC5√15mD25√5mA particle is fired from A in the diagonal plane of a building of dimension 20m(length) × 15m (breadth) × 12.5m(height), just clears the roof diagonally & falls on the other side of the building at B.It is observed that the particle is travelling at an angle 45∘ with the horizontal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
The speed of projection of the particle at A will be:
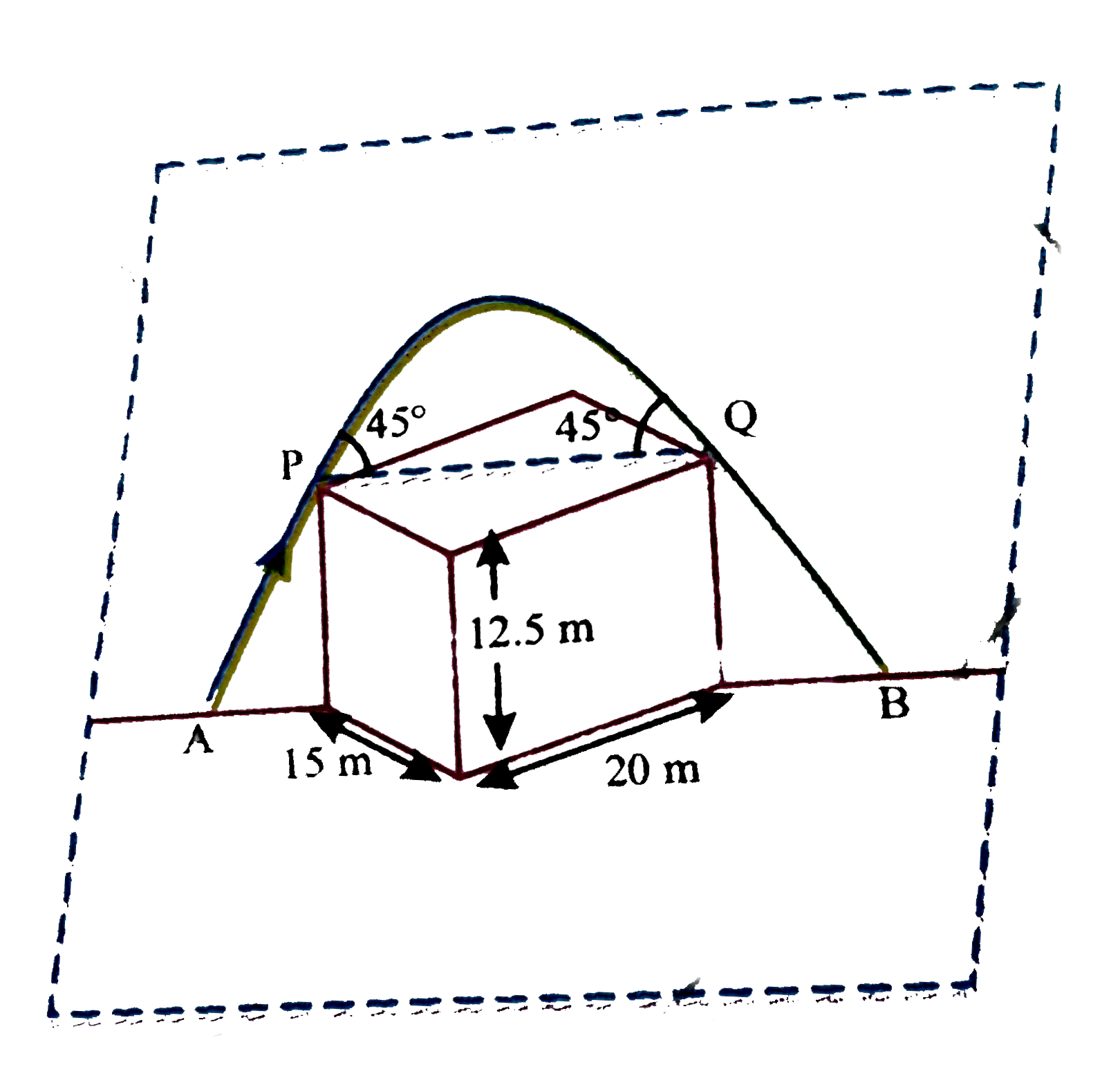 A5√10m/sB10√5m/sC5√15m/sD5√5m/s
A5√10m/sB10√5m/sC5√15m/sD5√5m/s
A particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle θ with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionA rod of mass M=5kg and length L=1.5m is held vertical on a table as shown. A gentle push is given to it and it starts falling. Friction is large enough to prevent end A from slipping on the table.
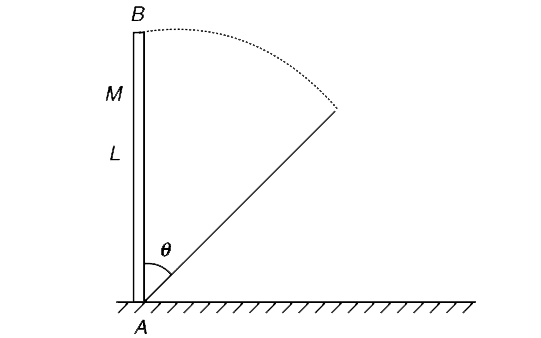
(a) Find the sum of linear momentum of all the particles of the rod when it rotates through an angle θ=37∘
(b) Find the friction force and normal reaction force by the table on the rod, when θ=37∘
(c) Find value of angle q when the friction force becomes zero.
[tan37∘=34 and g=10m/s]
View SolutionA particle is fired from A in the diagonal plane of a building of dimension 20m(length) × 15m (breadth) × 12.5m(height), just clears the roof diagonally & falls on the other side of the building at B.It is observed that the particle is travelling at an angle 45∘ with the horizontal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
The speed of the particle at point P will be:
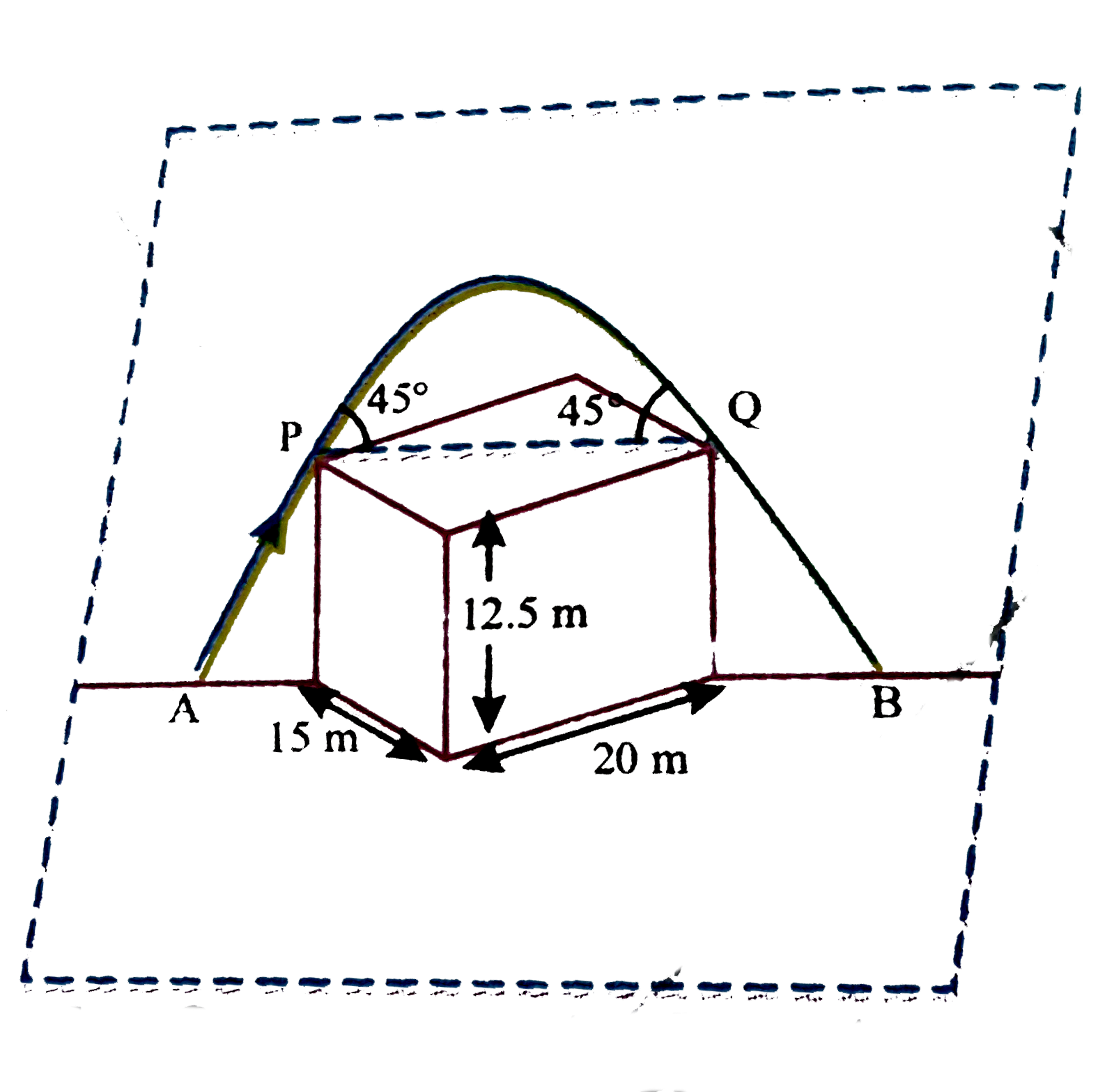
View SolutionA particle is fired from 'A' in the diagonal plane of a building of dimension 20m (length)×15m (breath) xx12.5m (height), just clears the roof diagonally and falls on the other side of the building at B. It is observed that the particle is travelling at an angle 45∘ with the horizonal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
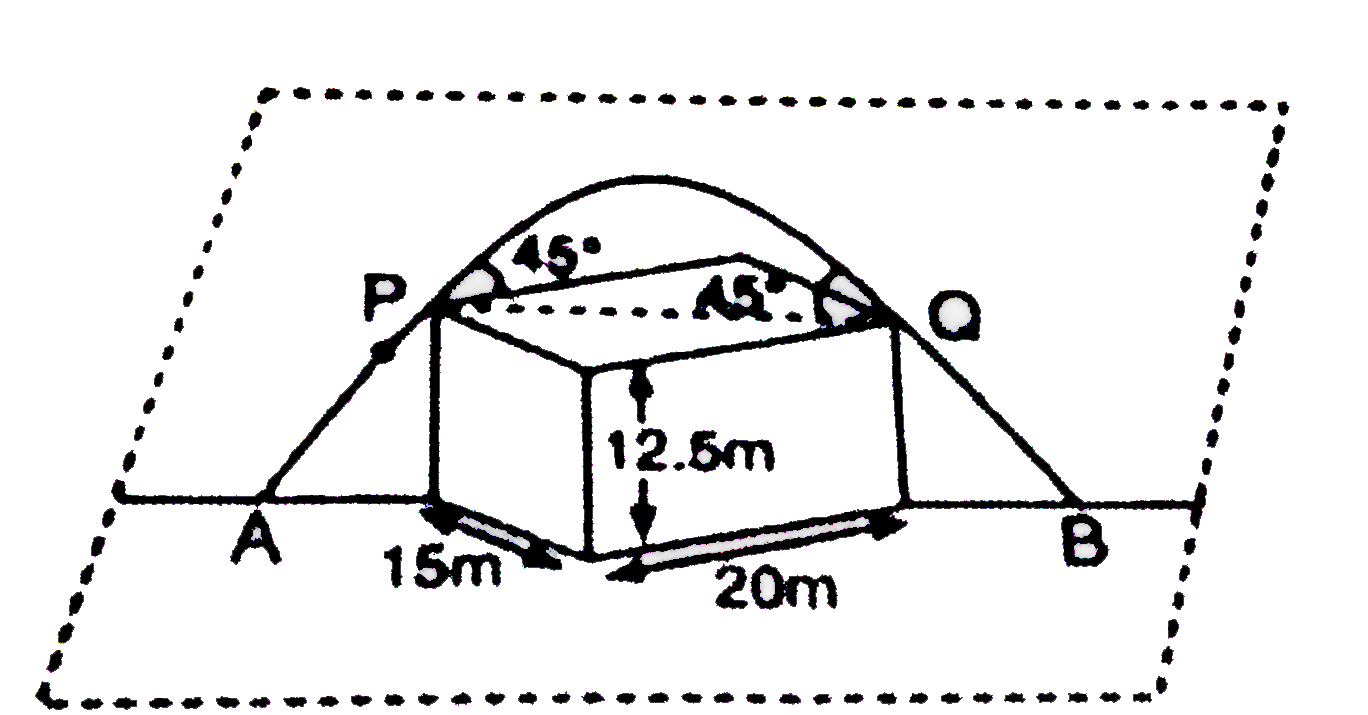
The range that is AB will be:
View SolutionA particle is fired from 'A' in the diagonal plane of a building of dimension 20m (length)×15m (breath) xx12.5m (height), just clears the roof diagonally and falls on the other side of the building at B. It is observed that the particle is travelling at an angle 45∘ with the horizonal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
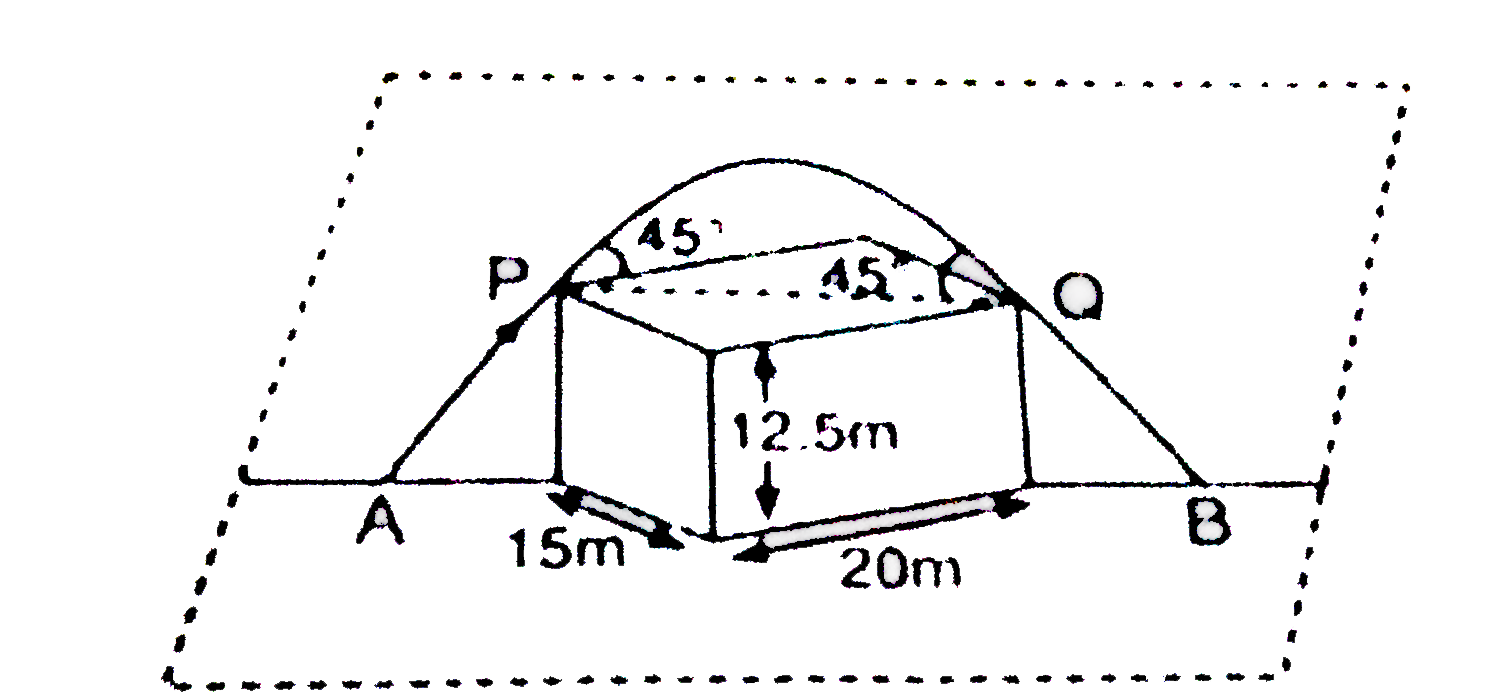
The speed of projection of the particle at A will be:
View Solution
