A sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
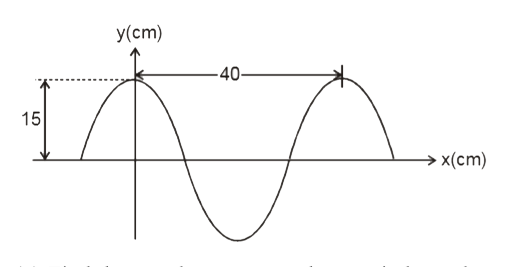
(b) Determine the phase constant ϕ, and write a general expression for the wave function.
π2,cos(16πt−π20x)
0,sin(16πt−π20x)
π2,sin(16πt−π20x)
π4,sin(16πt−π20x+π4)
The correct Answer is:A
Initial phase constant is π2, y=Asin(ωt−kx)
Related Playlists
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-III56videos
WAVES
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-IV56videos
WAVES
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-II (C.W)15videos
WAVES
- BOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)14videos
VECTORS
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV43videos
WORK , ENERGY & POWER
Similar Questions
A sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
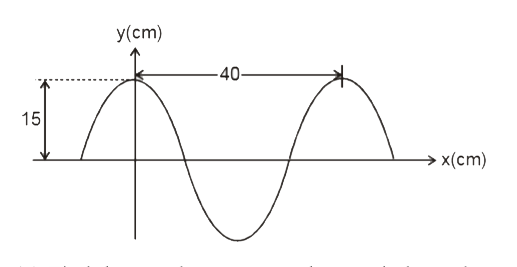
(a) Find the angular wave number, period angular frquency and speed of the wave.View SolutionA sinusoidal wave travelling in the positive x direction has an amplitude of 15cm, wavelength 40cm and freqency 8Hz. The vertical displacement of the medium at t=0 and x=0 os also 15cm, as shown.
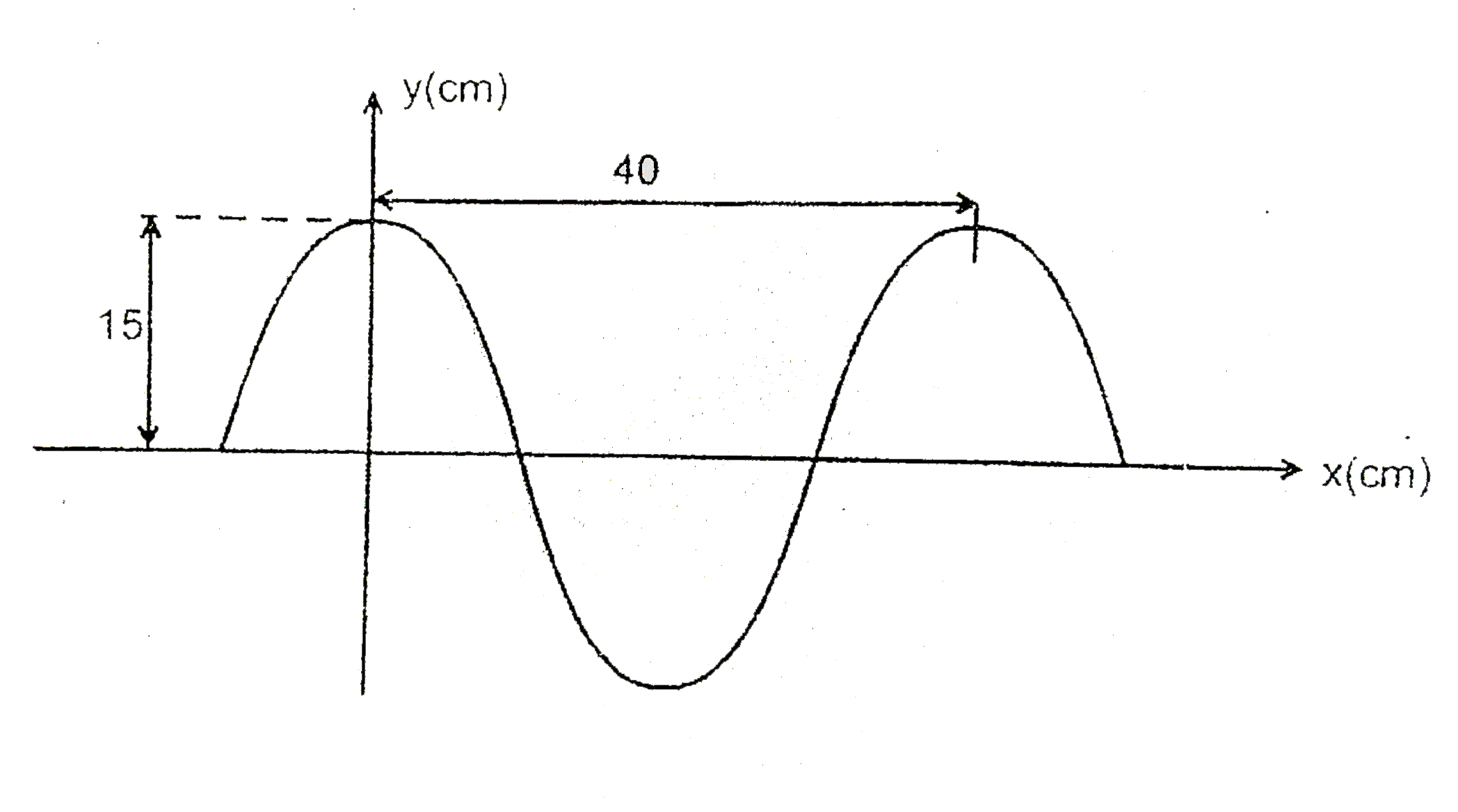
(a) Find the angular wave number, period, angualr frequency and speed of the wave.
(b) Datermine the phase constant ϕ, and write a general expression for the two wave function.View SolutionA sinusoidal wave travelling in the positive x-direction has an amplitude of 15.0cm, a wavelength of 40.0cm and a frequency of 8.00Hz.Thevertic≤displacementofthemediumatt = 0 and x = 0isalso15.0 cmasshown∈figure.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V03_C17_E01_054_Q01.pngwh=80%mx-autosty≤=background:white;><br>(a)F∈dtheanga––rwaveνmberk,periodT,anga––requencyomegaandspeedv of the wave.
(b) Write a general expression for wave function.View SolutionA sinusoidal wave trsvelling in the positive direction on a stretched string has amplitude 2.0cm, wavelength 1.0cm and velocity 5.0m/s. At x=0 and t=0 it is given that y=0 and ∂y∂t<0. Find the wave function y(x,t).
View SolutionA progressive wave is travelling along the positive direction of the x-axis. For this wave, amplitude = 5 cm, period = 0.2 s and wavelength = 30 cm
The equation of the wave using SI units is given byView SolutionA wave is propagating along the positive direction of X-axis. If the amplitude of wave is 10 cm, frequency 200 Hz and velocity 400 m/s, then write the equation of progressive wave.
View SolutionA transverse wave, whose amplitude is 0.5 m wavelength is 1 m and frequency is 2Hz. is travelling along positive x direction. The equation of this wave will be-
View SolutionWrite the equation of a progressive wave propagating along the positive x-direction, whose amplitude is 5cm, frequency 250Hz and velocity 500 m/ s.
View SolutionA longitudinal harmonic wave is travelling along positive x direction. The amplitude, wavelength and frequency of the wave are 8.0×10–3m,12cm and 6800Hz respectively. The displacement (s) versus position graph for particles on the x axis at an instant of time has been shown in figure. Find the separation at the instant shown, between the particles which were originally at x1=1cm and x2=3cm
 View Solution
View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is
View Solution


