In (Q. 24.) the tension in string is T and the linear mass density of string is $μ$ . The ratio of magnitude of maximum velocity of particle and the magnitude of maximum acceleration is

$\frac{1}{2 π} \sqrt{(\frac{μ l^{2}}{T})}$

$2 π \sqrt{(\frac{μ l^{2}}{T})}$

$\frac{1}{2 π} \sqrt{(\frac{T}{μ l^{2}})}$

$\frac{1}{4 π} \sqrt{(\frac{μ l^{2}}{T})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

The magnitude of maximum acceleration of car occurs at

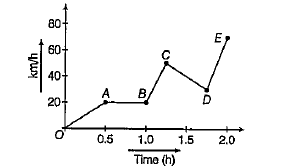AOA
BBC
CCD
DDE
The speed on string with tension T and linear mass density $μ$ is -
A $V = \sqrt{\frac{T}{μ}}$
B $V = \sqrt{\frac{B}{ρ}}$
C $V = \sqrt{\frac{Y}{ρ}}$
DNone of these
The linear mass density $' μ'$ of the string is (where, mass of the string = m, length of the string = L)
A $\frac{m}{L}$
BmL
C $m t^{2}$
D $\frac{m}{L_{3}}$