A standing wave, having 5 nodes and 4 antinodes is formed between two atoms having a distance 1.21Å between them. The wavelength of the standing wave is
1.21Å
2.42Å
6.05Å
0.605Å
The correct Answer is:D
To find the wavelength of the standing wave formed between two atoms that are 1.21 Å apart, with 5 nodes and 4 antinodes, we can follow these steps:
1. Understanding Nodes and Antinodes:
- In a standing wave, nodes are points where there is no displacement, while antinodes are points of maximum displacement.
- The given standing wave has 5 nodes and 4 antinodes.
2. Identifying the Relationship:
- The number of nodes (N) and antinodes (A) in a standing wave is related by the formula:
N=A+1
- Here, we have 5 nodes and 4 antinodes, which confirms the relationship:
5=4+1
3. Calculating the Number of Wavelengths:
- The distance between two consecutive nodes is half a wavelength (λ/2).
- The total distance between the first and the last node (5 nodes) can be calculated as:
Total distance=Number of intervals between nodes×λ2
- The number of intervals between 5 nodes is 4 (since there are 4 gaps between 5 nodes).
4. Setting Up the Equation:
- Therefore, the total distance between the two atoms (1.21 Å) can be expressed as:
1.21 \, \text{Å} = 4 \times \frac{\lambda}{2}
- Simplifying this gives:
1.21Å=2λ
5. Solving for Wavelength (λ):
- Rearranging the equation to find λ:
λ=1.21Å2=0.605Å
Final Answer:
The wavelength of the standing wave is 0.605 Å.
---
- In a standing wave, nodes are points where there is no displacement, while antinodes are points of maximum displacement.
- The given standing wave has 5 nodes and 4 antinodes.
- The number of nodes (N) and antinodes (A) in a standing wave is related by the formula:
N=A+1
- Here, we have 5 nodes and 4 antinodes, which confirms the relationship:
5=4+1
- The distance between two consecutive nodes is half a wavelength (λ/2).
- The total distance between the first and the last node (5 nodes) can be calculated as:
Total distance=Number of intervals between nodes×λ2
- The number of intervals between 5 nodes is 4 (since there are 4 gaps between 5 nodes).
- Therefore, the total distance between the two atoms (1.21 Å) can be expressed as:
1.21 \, \text{Å} = 4 \times \frac{\lambda}{2}
- Simplifying this gives:
1.21Å=2λ
- Rearranging the equation to find λ:
λ=1.21Å2=0.605Å
The wavelength of the standing wave is 0.605 Å.
Topper's Solved these Questions
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-I (H.W)
101 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-II (C.W)
15 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - C.U.Q
68 Videos
- VECTORSBOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)
14 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV
43 Videos
Similar Questions
A standing wave having 3 nodes and 2 antinodes is formed between two atoms having a distance 1.21Å between them. The wavelength of the standing wave is
View SolutionIn a standing wave 4 nodes and 3 antinodes are formed between two fixed end of string of length 6 m. Then the wave length of the standing wave is
View Solution
Knowledge Check
A standing wave having 3 nodes and 2 antinodes is formed between two atoms having a distance 1.21Å between them. The wavelength of the standing wave is
A1.21ÅB1.42ÅC6.05ÅD3.63ÅA standing wave having 3 nodes and 2 antinodes is formed between two atoms having a distance 1.21Å between them. The wavelength of the standing wave is
A6.05ÅB2.42ÅC1.21ÅD3.63ÅA standing wave having 3 nodes and 2 antinodes are formed between two rigid supports of length 1m. Then the wavelength of the standing wave is
A0.5mB1.0mC0.75mD0.25m
For a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
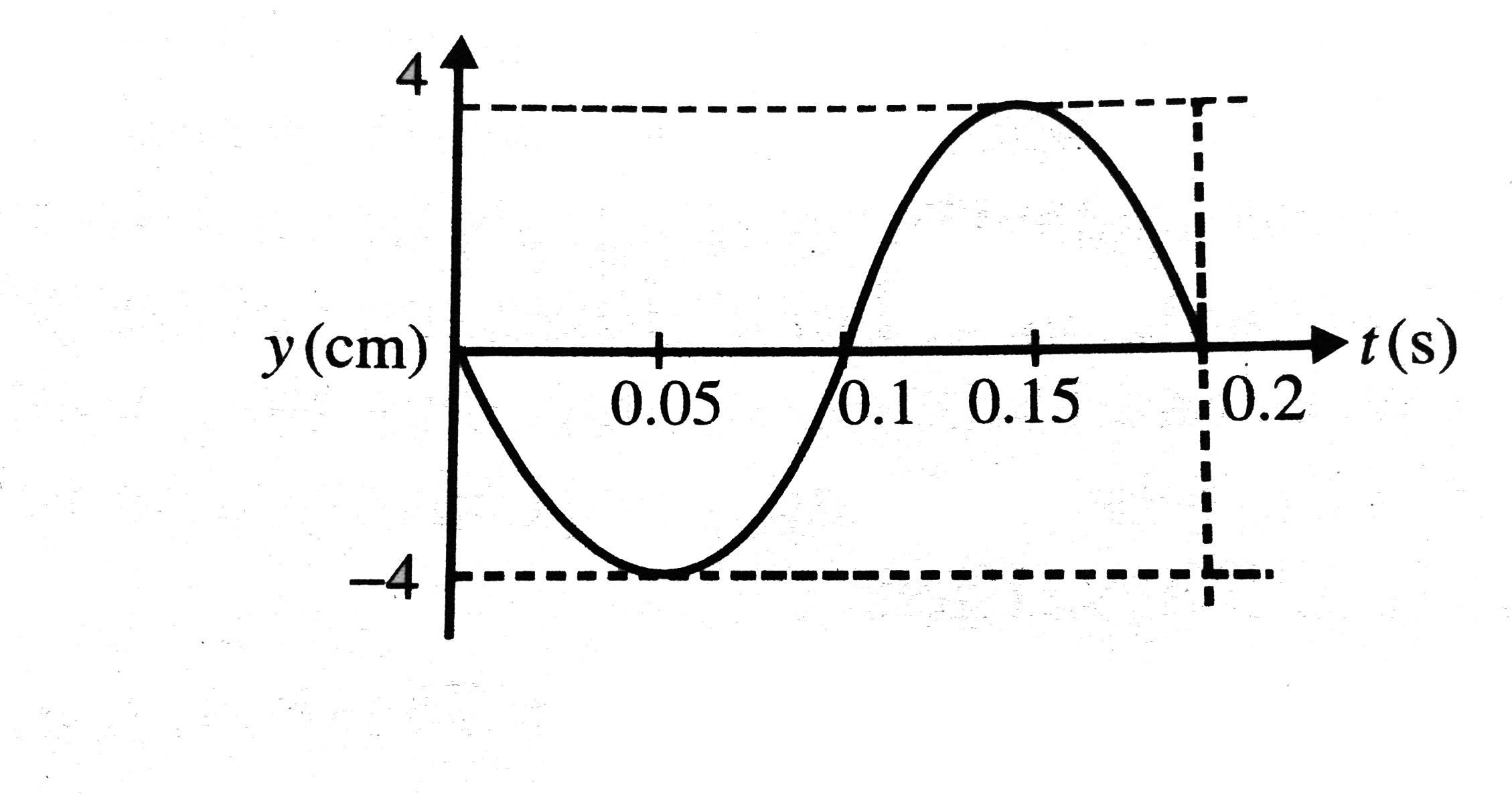
View SolutionThe string fixed at both ends has standing wave nodes for which distance between adjacent nodes is x1. The same string has another standing wave nodes for which distance between adjacent nodes is x2. If l is the length of the string then x2/x1=l(l+2x1). What is the difference in numbers of the loops in the two cases?
View SolutionThe distance between any two successive nodes or antinodes in stationary waves is
View SolutionA standing wave in a string 35 cm long has a total of six nodes including those at the ends. Hence, wavelength of the standing wave is
View SolutionWavelength of wave is a distance between two particles in phase differing by
View Solution
