A plane progressive wave cannot be represented by
y=asin(ωt±kx)
y=asin2π(tT−+xλ)
y=asin.2πλ(Vt−+x)
y=Alogx+Blogx
The correct Answer is:D
To determine which equation cannot represent a plane progressive wave, we need to understand the characteristics of such waves and their equations.
1. Understand the Definition of a Plane Progressive Wave:
- A plane progressive wave is a wave that propagates in a single direction and exists in a single plane. It can be described mathematically as a function of both position and time.
2. Identify the Characteristics of the Wave Equation:
- The general form of a plane progressive wave can be expressed as y(x,t)=Asin(kx−ωt+ϕ) or y(x,t)=Acos(kx−ωt+ϕ), where:
- y is the displacement,
- A is the amplitude,
- k is the wave number,
- x is the position,
- ω is the angular frequency,
- t is the time,
- ϕ is the phase constant.
3. Check the Given Options:
- Evaluate each option to see if it includes both position (x) and time (t):
- Option 1: Contains both x and t → Valid.
- Option 2: Contains both x and t → Valid.
- Option 3: Contains both x and t → Valid.
- Option 4: Contains logx and lacks t → Invalid.
4. Conclusion:
- The equation that cannot represent a plane progressive wave is the one that does not include time. Therefore, the answer is the equation with logx and no time component.
Final Answer:
The equation that cannot represent a plane progressive wave is the one that contains logx without a time variable.
---
- A plane progressive wave is a wave that propagates in a single direction and exists in a single plane. It can be described mathematically as a function of both position and time.
- The general form of a plane progressive wave can be expressed as y(x,t)=Asin(kx−ωt+ϕ) or y(x,t)=Acos(kx−ωt+ϕ), where:
- y is the displacement,
- A is the amplitude,
- k is the wave number,
- x is the position,
- ω is the angular frequency,
- t is the time,
- ϕ is the phase constant.
- Evaluate each option to see if it includes both position (x) and time (t):
- Option 1: Contains both x and t → Valid.
- Option 2: Contains both x and t → Valid.
- Option 3: Contains both x and t → Valid.
- Option 4: Contains logx and lacks t → Invalid.
- The equation that cannot represent a plane progressive wave is the one that does not include time. Therefore, the answer is the equation with logx and no time component.
The equation that cannot represent a plane progressive wave is the one that contains logx without a time variable.
Topper's Solved these Questions
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-I (C.W)
104 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-I (H.W)
101 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Evaluate yourself-5
7 Videos
- VECTORSBOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)
14 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV
43 Videos
Similar Questions
Knowledge Check
A plane progressive wave is represented by the equation y=0.25cos(2πt−2πx) The equation of a wave is with double the amplitude and half frequency but travelling in the opposite direction will be :-
Ay=0.5cos(πt−πx)By=0.5cos(2πt+2πx)Cy=0.25cos(πt+2πx)Dy=0.5cos(πt+πx)A plane progressive wave is represented by the equation y=0.1sin(200pot−20πx17)where y is displacement in m , t in second and x is distance from a fixed origin in meter . The frequency, wavelength and speed of the wave respectively are
A100Hz,1.7m,170m/sB150Hz,2.4m,200m/sC80Hz,1.1m,90m/sD120Hz,1.25m,207m/sAssertion : A progressive wave can be represented by y=log(x+vt)
Reason: Any progressive wave must have the form y=f(x−vt)ory=f(x+vt) where symbols have their usual meaningAAssertion is True Reason is True, Reason is a correct explanation for AssertionBAssertion is True Reason is True : Reason is not a correct explanation for AssertionCAssertion is True ,Reason is FalseDAssertion is False but , Reason is True
The displacement of a progressive wave is represented by y=Asin(ωt−kx), where x is distance and t is time. Write the dimensional formula of (i) omega and (ii) k.
View SolutionSelect and write the corrcet answer :
A simple harmonic progressive wave is represented by y=0.01sin4π(t−x2) in SI units. The wavelength of the wave is
View SolutionA simple harmonic progressive wave is represented by y=Asin(100πt+3x).The distance between two points on the wave at a phase difference of π3 radian is
View SolutionThe same progressive wave is represented by two graphs I and II. Graph I shows how the displacement 'y' varies with the distance x along the wave at a given time. Graph I shows how y varies with time t at a given point on the wave. The ratio of measurements AB to CD, marked on the curves, represents :
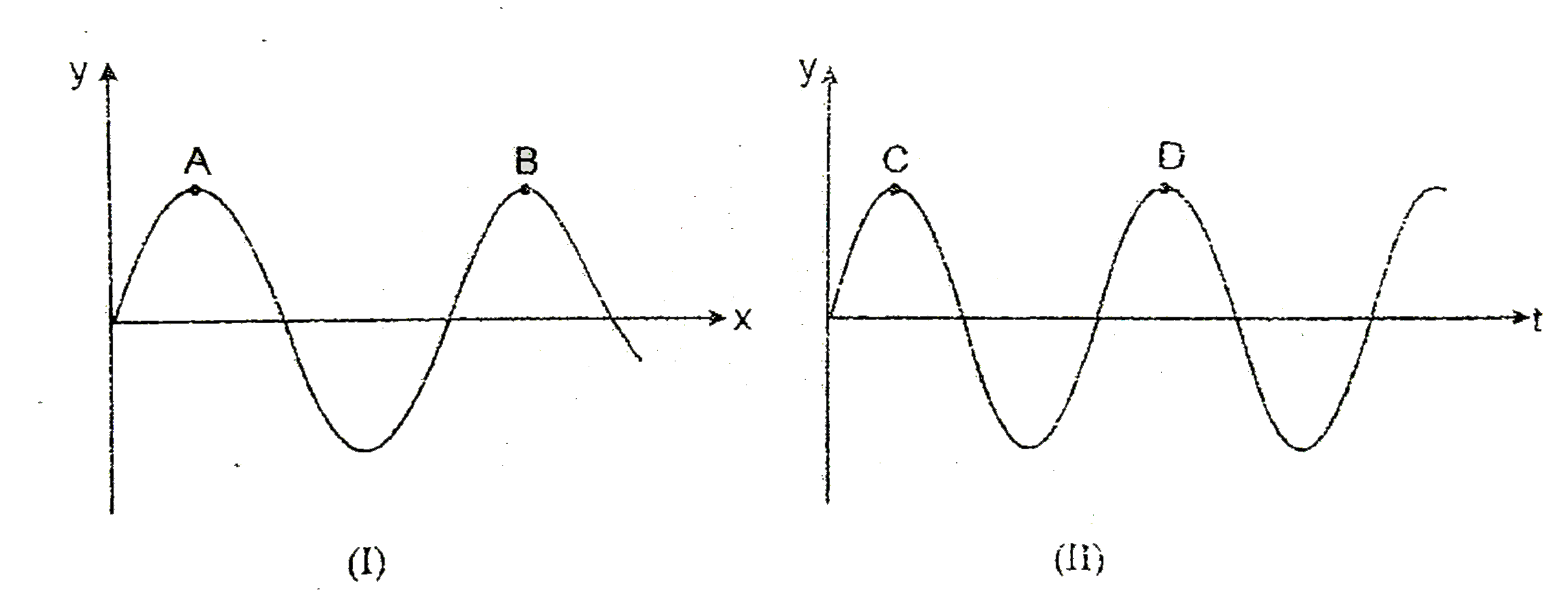
View Solution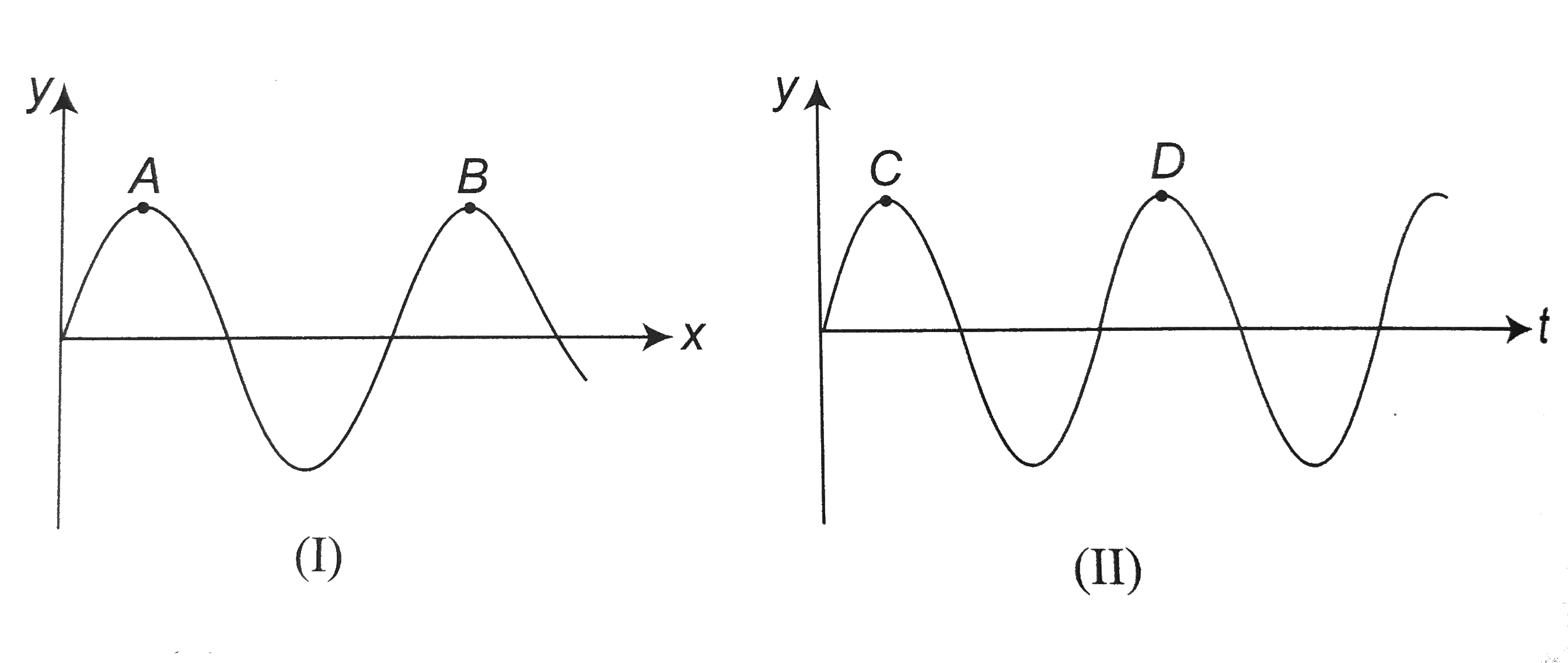
The same progressive wave is represented by two graphs I and II. Graph I shows how the displacement y varies with the distance x along the wave at a given time. Graph II shows how y varies with time t at a given point on the wave. The ratio of measurements AB to CD, marked on the curves represents:
View Solution
