A thin rod of length L and mass M is bent at its midpoint into two halves so that the angle between them is 90∘. The moment of inertia of the bent rod about an axis passing through the bending point and perpendicular to the plane defined by the two halves of the rod is.
ML224
ML212
ML26
√2ML224
The correct Answer is:B
Since rod is bent at the middle , so each part of it will have same length (L2) and msss (M2) as shown .

The moment of inertia of each part through its one end =13(M2)(L2)2 , Hence , net moment pof inrtia through its middle point O is
I=13(M2)(L2)2+13(M2)(L2)2
=13[ML28+ML28]=ML212
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - II (H.W)
Explore 60 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
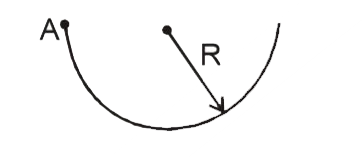
A uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is
View SolutionA thin rod of length l and mass m is turned at mid-point O at angle of 60°. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
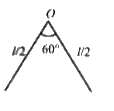
View Solution
Knowledge Check
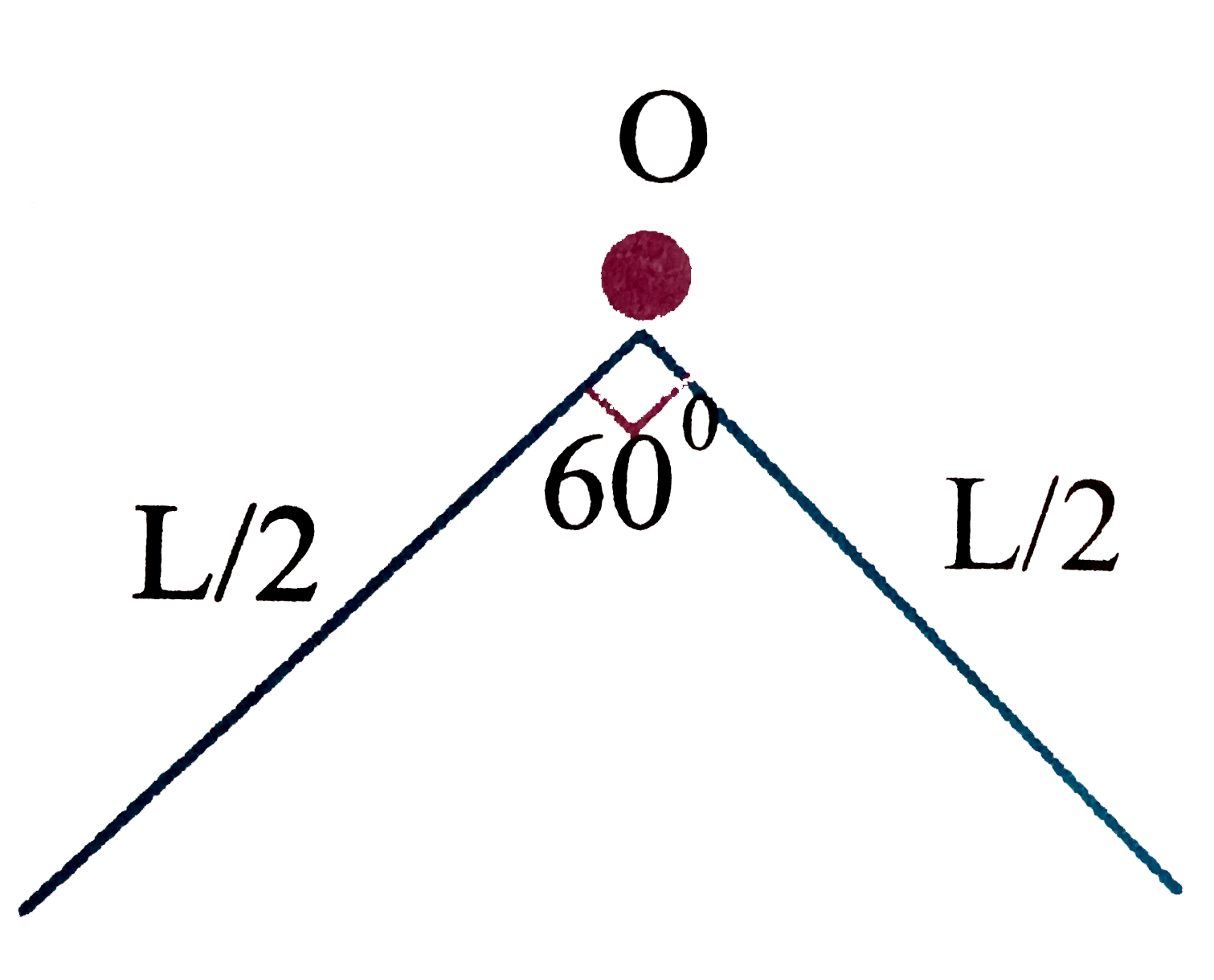
A thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
 AML26BML212CML224DML23
AML26BML212CML224DML23A thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
 AML26BML212CML224DML23
AML26BML212CML224DML23The moment of inertia of thin rod of linear density λ and length l about an axis passing through one end and perpendicular to its length is
Aλl212Bλl23Cλl312Dλl33

A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?
View SolutionA uniform rod of mass 2M is bent into four adjacent semicircles each of radius r, all lying in the same plane. The moment of inertia of the bent rod about an axis through one end A and perpendicular to plane of rod is

View SolutionTwo rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
View SolutionTwo rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
View SolutionTwo rods each of mass m and length 1 are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them, is :
View Solution

