A wheel is rolling uniformly along a level road without slipping . Velocity of the highest point on its rim about the road is V . Then magnitude of velocity of a point on its rim which is at the same level as that of the centre is
√2V
V/2
2V
V/√2
The correct Answer is:D
To solve the problem step-by-step, we need to analyze the motion of the wheel and the velocities of the points on its rim.
Step 1: Understand the motion of the wheel
The wheel is rolling uniformly along a level road without slipping. This means that every point on the rim of the wheel has both translational and rotational motion.
Step 2: Identify the velocities
1. The velocity of the highest point on the rim (let's call it point A) is given as V.
2. We need to find the magnitude of the velocity of a point on the rim that is at the same level as the center of the wheel (let's call this point B).
Step 3: Relate translational and rotational motion
Let V0 be the translational velocity of the center of the wheel. In pure rolling motion, the relationship between the translational velocity V0 and the angular velocity ω is given by:
V0=ωR
where R is the radius of the wheel.
Step 4: Analyze the velocities of point B
Point B is at the same level as the center of the wheel. It has two components of velocity:
1. Translational velocity: This is equal to V0.
2. Rotational velocity: The tangential velocity due to rotation about the center of the wheel. Since point B is at a distance R from the center, the tangential velocity is also V0.
Step 5: Calculate the resultant velocity of point B
The total velocity of point B is the vector sum of its translational and rotational velocities. Since both velocities are in the same direction, we can add them directly:
VB=V0+V0=2V0
Step 6: Substitute V0 in terms of V
From the information given, we know that the velocity of the highest point (point A) is V. Since point A is also moving with the same angular velocity, we can express V0 in terms of V:
V=V0+V0=2V0⟹V0=V2
Step 7: Substitute V0 back into the equation for point B
Now substituting V0 back into the equation for the velocity of point B:
VB=2V0=2(V2)=V
Final Answer
The magnitude of the velocity of the point on the rim which is at the same level as that of the center is:
V
The wheel is rolling uniformly along a level road without slipping. This means that every point on the rim of the wheel has both translational and rotational motion.
1. The velocity of the highest point on the rim (let's call it point A) is given as V.
2. We need to find the magnitude of the velocity of a point on the rim that is at the same level as the center of the wheel (let's call this point B).
Let V0 be the translational velocity of the center of the wheel. In pure rolling motion, the relationship between the translational velocity V0 and the angular velocity ω is given by:
V0=ωR
where R is the radius of the wheel.
Point B is at the same level as the center of the wheel. It has two components of velocity:
1. Translational velocity: This is equal to V0.
2. Rotational velocity: The tangential velocity due to rotation about the center of the wheel. Since point B is at a distance R from the center, the tangential velocity is also V0.
The total velocity of point B is the vector sum of its translational and rotational velocities. Since both velocities are in the same direction, we can add them directly:
VB=V0+V0=2V0
From the information given, we know that the velocity of the highest point (point A) is V. Since point A is also moving with the same angular velocity, we can express V0 in terms of V:
V=V0+V0=2V0⟹V0=V2
Now substituting V0 back into the equation for the velocity of point B:
VB=2V0=2(V2)=V
The magnitude of the velocity of the point on the rim which is at the same level as that of the center is:
V
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - III
43 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - II (C.W)
60 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
During rolling without slipping, what is the velocity of the point in contact with the surface.
View SolutionA wheel is rolling uniformly along a level road (see figure). The speed of transitional motion of the wheel axis is V. What are the speeds of the points A and B on the wheel rim relative to the road at the instant shown in the figure?
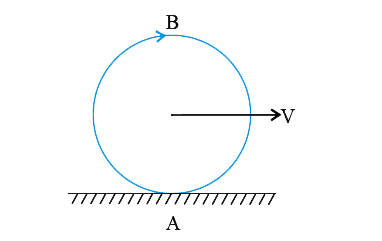
View Solution
Knowledge Check
A circular disc rolls on a horizontal floor without slipping and the center of the disc moves with a uniform velocity v. Which of the following values of the velocity at a point on the rim of the disc can have?
AvB−vC3DZeroA wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is vCM, then true statement is
 AThe velocity of point A is 2vCM and velocity of point B is zeroBThe velocity of point A is zero and velocity of point B is 2vCMCThe velocity of point A is 2vCM and velocity of point B is −vCMDThe velocities of both A and V are vCM
AThe velocity of point A is 2vCM and velocity of point B is zeroBThe velocity of point A is zero and velocity of point B is 2vCMCThe velocity of point A is 2vCM and velocity of point B is −vCMDThe velocities of both A and V are vCMA circular disc rolls on a horizontal floor without slipping and the centre of the disc moves with a unifonn velocity v. Which of the following values the velocity at a point on the rim of the disc can have?
AvB−vC2vDzero
A wheel is rolling straight on ground without slipping. If the axis of the wheel has speed v, the instantenous velocity of a point P on the rim, defined by angle θ, relative to the ground will be

View SolutionA disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.

View SolutionA wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
View SolutionA cotton reel rolls without sliding such that the point P of the string has velocity v=6m/s. If r=10cm and R=20cm then the velocity of its centre C is.
 .
.
View SolutionA uniform ring rolls on a horizontal surface with out slipping. Its centre of mass moves with a constant speed v. then speed of the upper most point on its rim above the ground is
View Solution
