Suppose, we have to find out modal marks from the following frequency distribution: (Table 8.8)

l1=40,
Δ1=20−9=11
Δ2=20−10=10,
i=20(=40−20)
Substituting these values
Mode =l1+Δ1Δ1+Δ2×i=40+1111+10×20=40+1121×20
=40+22021=40+10.8 approx=50.48 approx.
Topper's Solved these Questions
- MEDIAN AND MODEBook:SK AGGARWALAChapter:MEDIAN AND MODEExercise:Multiple Choice Questions
Explore 5 Videos
- MEDIAN AND MODEBook:SK AGGARWALAChapter:MEDIAN AND MODEExercise:Numerical Problem
Explore 21 Videos
- MEDIAN AND MODEBook:SK AGGARWALAChapter:MEDIAN AND MODEExercise:Numerical Problem
Explore 21 Videos
- MEASURES AND DISPERSIONBook:SK AGGARWALAChapter:MEASURES AND DISPERSIONExercise:Numerical Questions
Explore 18 Videos
- OTHER FORMS OF MARKETBook:SK AGGARWALAChapter:OTHER FORMS OF MARKETExercise:SAMPLE PAPER
Explore 29 Videos
Similar Questions
Find the mean marks from the following frequency distribution

View SolutionFind the median marks for the following frequency distribution :

View SolutionWrite the modal class for the following frequency distribution.
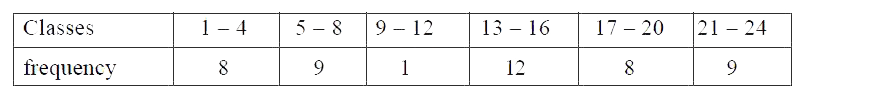
View SolutionDetermine the upper limit of the modal class of the following frequency distribution:

View SolutionFind out the standard deviation from the following distribution table:
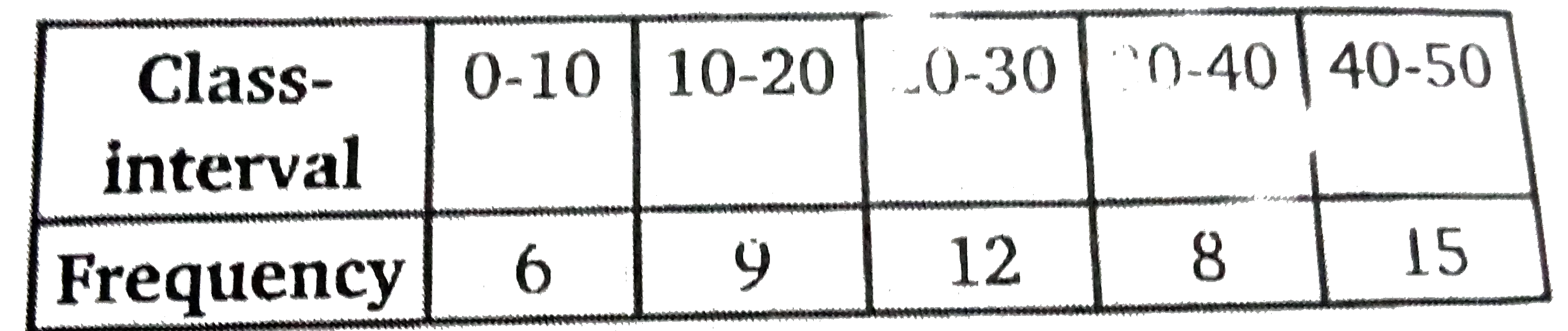
View SolutionFind out the standard deviation from the following distribution table:

View SolutionIf the mean of the following frequency distribution is 8, find the value of p

View SolutionFind D8 and P40 from the following distribution:

View SolutionFind out the mode from the following frequency distribution: Central sizes : 12345678910 Frequency : 86101220125324
View SolutionFrom the frequency distribution table from the following data

View Solution
