तीन सकेंद्रिये गोलिये कोशो की त्रिज्ये a,b व् c(a<b<c) हैं तथा पृष्ठि आवेश घनत्व क्रमश :σ−σ तथा σ है। यदि VA,VB तथा VC तीनो कोशो के विभव हैं, तब c=a+b के लिए,
VA=VC≠VB
VC=VB≠VA
VC≠VB≠VA
VC=VB=VA
The correct Answer is:A
a त्रिजिया के गोले पर विभव तीनो गोलों के विभव का योग होगा। ∵ आवेशित गोले की सतह पर विभव का सूत्र,
V=14πε0qR2 (यहाँ, ε0 = निर्वार्त की विधतुशीलता, q = सतह पर आवेश व R = त्रिजिया )
यहाँ: VA=14πε0σ4πa2a−14πε0σ4πb2b+14πε0σ4πc2c
= σε0(a−b+c)=σε0(2a) (∵ c = a+b) ...(i)
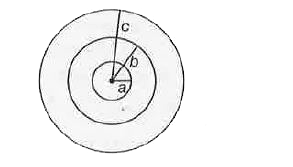
∵ किसी गोलिये कोष के अंदर विभव नियत व सतह के समान होता है। इसी प्रकार त्रिजिया के गोले पर विभव,
VB=14πε0σ4πa2b−14πε0σ4πb2b+14πε0.σ4πc2c
σε0(a2b−b+c)=σε0(a2b+a) ...(ii)
(∵ c = a + b)
तथा .c. त्रिजिया के गोले पर विभव ,
Vc=14πε0.σ4πa2c−14πε0σ4πb2c+14πε0.σ4πc2c
σε0(a2c−b2c+(c))=σε0(2a)...(iii)
(∵ c = a + b)
तीनो समीकरणों से स्पष्ट है की प्रतिबंध c = a+b के लिए VA=VC≠VB होगा।
Topper's Solved these Questions
Similar Questions
एक 4μF के संधारित्र को 400 V पर आवेशित किया गया तथा इसकी प्लेटों को KΩ वाले प्रतिरोध से जोड़ दिया गया। बताओ प्रतिरोध में कितनी ऊष्मा बनेगी?
View Solution5×10−8C तथा −3×10−5C के दो आवेश 16 सेमि की दुरी पर स्थित है। दोनों आवेशों को मिलाने वाली रेखा के किस बिंदु पर विभव शून्य है? अंतर पर विभव शून्य लीजिए।
View SolutionThree concentric spherical metallic shells A, B, and C of radii a,b, and c(a lt b lt c) have surface charge densities sigma, -sigma and sigma , respectively. If V_(A), V_(B) and V_(C) are potential of shells A, B and C, respectively, match the columns {:("Column A",,,"Column B"),(a. V_(A),,i.,sigma/epsilon_(0)[(a^(2)-b^(2)+c^(2))/c]),(b. V_(B),,ii.,sigma^(2)/epsilon_(0)[a^(2)/b-b+c]),(c. V_(C),,iii.,sigma/epsilon_(0)[a-b+c]):}
View SolutionThree concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−σandσ respectively. If VA,VB and VC denote the potentials of the three shells, then for c=a+b, we have
View SolutionThree concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−σ and σ respectively. If VA,vB and Vc denote the potentials of the three shells, then, for VA=VC, we get-
View Solutionतीन संकेन्द्री धातु कोष A , B तथा C जिनकी त्रिज्याये क्रमशः a , b तथा c(a<b<c) है, पृष्ठ -आवेश-घनत्व क्रमशः +σ,−σ तथा +σ है कोष B का विभव होगा :
View SolutionThree concentric metal shells A, B, and C of respective radii a,b and c (a lt b lt c) have surface charge densities +σ,−σand+σ respectively. The potential of shell B is
View SolutionThree concentric spherical metallic shells A,B and C of radii a,b and c (a<b<c) have surface charge densities σ,−σandσ respectively.
If the potenital of sheel B is VB=σ∈0(anb−b+c) and the potential of shell C is VC=σ∈0(anc−bnc+c) then n is .
View SolutionThree concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities σ, −σ and σ respectively.
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.
View SolutionA,B,C तीन अशून्य सदिश हैं जिनमें कोई भी दो समान्तर नहीं हैं। यदि A+ B सदिश C के समरेख तथा B+ C सदिश A के समरेख हो, तो A+ B+C बराबर है
View Solutionयदि a तथा b इकाई सदिश हैं तथा θ इनके बीच का कोण है। तब ∣∣ˆa+ˆb∣∣<1 यदि
View Solutionतीन संकेद्रीय गोलीय कोश की त्रिज्याएँ a, b व c(a<b<c) हैं तथा इनके आवेश पृष्ठ घनत्व क्रमशः σ,−σवσ हैं | यदि VA,VBवVC तीनों गोलीय कोश के विभव हों , तब c = a + b , के लिये है
View SolutionConsider A, D and C to be the co-centric shells of metal . Their radii are a ,b and c respectively (a < b < c). Their surface charge densities are σ,−σ and σ respectively. Calculate the electric potential on the surface of shell A.
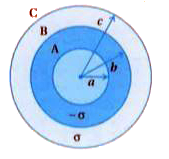
View SolutionThree concentric spherical shells have radii a, b and c(a lt b lt c) and have surface charge densities sigma, -sigam and sigma respectively. If V_(A), V_(B) and V_(C) denote the potentials of the three shells, then for c = a + b , we have
View Solutiona, b एवं c (a < b < c) त्रिज्या के तीन सकेन्द्रीय धात्विक कोष के पृष्ठ आवेश घनत्व क्रमशः −σ,+σ एवं −σ है। कोष A पर विभव होगा।
View SolutionThree concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−σ and σ respectively. If VA,VB and VC denote the potentials of the three shells, then for c=q+b, we have
View Solution