Three concentric spherical metallic shells A,B and C of radii a,b and c (a<b<c) have surface charge densities σ,−σandσ respectively.
If the potenital of sheel B is VB=σ∈0(anb−b+c) and the potential of shell C is VC=σ∈0(anc−bnc+c) then n is .
The correct Answer is:2
To solve the problem, we need to find the value of n given the potentials VB and VC of the concentric spherical metallic shells A, B, and C.
1. Understanding the Setup:
We have three concentric spherical shells A, B, and C with radii a, b, and c respectively, where a<b<c. The surface charge densities are σ for shell A, −σ for shell B, and σ for shell C.
2. Potential of Shell B:
The potential VB is given by:
VB=σϵ0(anb−b+c)
3. Potential of Shell C:
The potential VC is given by:
VC=σϵ0(anc−bnc+c)
4. Finding the Charge Contributions:
- The potential VB is influenced by the charge on shell A and shell C (since shell B has a negative charge, it contributes negatively).
- The potential VC is influenced by the charges on shells A and B.
5. Expressing Potentials:
We can express both potentials in terms of the charge densities and the radii:
- For shell B:
VB=14πϵ0(σ⋅4πa2⋅1b−(−σ)⋅4πb2⋅1b+σ⋅4πc2⋅1b)
- For shell C:
VC=14πϵ0(σ⋅4πa2⋅1c−(−σ)⋅4πb2⋅1c+σ⋅4πc2⋅1c)
6. Comparing Potentials:
To find n, we need to compare the expressions for VB and VC. We can equate the coefficients of similar terms in both equations.
7. Finding n:
By comparing the terms in VB and VC:
- The term anb in VB corresponds to anc in VC.
- The term −b+c in VB corresponds to −bnc+c in VC.
From the comparison, we can derive that n=2.
Conclusion:
Thus, the value of n is:
2
We have three concentric spherical shells A, B, and C with radii a, b, and c respectively, where a<b<c. The surface charge densities are σ for shell A, −σ for shell B, and σ for shell C.
The potential VB is given by:
VB=σϵ0(anb−b+c)
The potential VC is given by:
VC=σϵ0(anc−bnc+c)
- The potential VB is influenced by the charge on shell A and shell C (since shell B has a negative charge, it contributes negatively).
- The potential VC is influenced by the charges on shells A and B.
We can express both potentials in terms of the charge densities and the radii:
- For shell B:
VB=14πϵ0(σ⋅4πa2⋅1b−(−σ)⋅4πb2⋅1b+σ⋅4πc2⋅1b)
- For shell C:
VC=14πϵ0(σ⋅4πa2⋅1c−(−σ)⋅4πb2⋅1c+σ⋅4πc2⋅1c)
To find n, we need to compare the expressions for VB and VC. We can equate the coefficients of similar terms in both equations.
By comparing the terms in VB and VC:
- The term anb in VB corresponds to anc in VC.
- The term −b+c in VB corresponds to −bnc+c in VC.
Thus, the value of n is:
2
Similar Questions
Three concentric metallic shells A , B and C of radii a, b and c (a<b<c) have surface densities +σ,−σ and +σ respectively as shown in Fig.
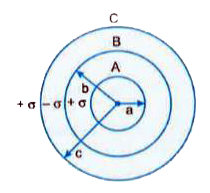
Obtain the expressions for the potential of three shells A , B and C .
View SolutionThree concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities σ, −σ and σ respectively.
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.
View Solution
Knowledge Check
Three concentric spherical metallic spheres A,B and C of radii a,b and c(a<b<c) have surface charge densities σ,−σ and σ respectively.
AThe potential of shell A:
VA=σε0(a+b+c)BThe potential of shell B:
VB=σε0(a2b−b+c)CThe potential of shell C:
VC=σε0(a2−b2c+c)DAll options are correctThree concentric metallic spherical shells A,B and C of radii a,band c(a<b<c) have surface charge densities −σ,+σand -sigma respectively,thepotentialofshellA is
A(σ/ε0)[a+b−c]B(σ/ε0)[a−b+c]C(σ/ε0)[b−a−c]DnoneThree concentric metallic spherical shell A,B and C or radiin a,b and C (a<b>C) have surface charge densities −singama,+σ, and −aigba respectively .
The potential of shell A is :A(σ/ɛ0)[a+b−c]B(σ/ɛ0)[a+b−c]C(σ/ɛ0)[a+b−c]Dnone
Three concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities σ, −σ and σ respectively.
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.
View SolutionThree concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities σ, −σ and σ respectively.
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.
View SolutionThree concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−σ and σ respectively. If VA,vB and Vc denote the potentials of the three shells, then, for VA=VC, we get-
View SolutionThree concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−σandσ respectively. If VA,VB and VC denote the potentials of the three shells, then for c=a+b, we have
View SolutionThree concentric spherical shells have radii a,b and c(a<b<c) and have surface charge densities σ,−sigam and σ respectively. If VA,VB and VC denote the potentials of the three shells, then for c=q+b, we have
View Solution

