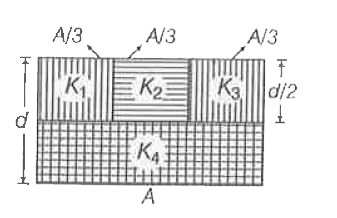
एक समांतर - पट्टिका संधारित्र का क्षेत्रफल A तथा इसकी धारिता C है। इसकी दो प्लेटो की बीच की दूरी है। इसमें क्रमश :, $K_{1}, K_{2}, K_{3}$ तथा $K_{4}$ परावैद्युतांक के चार पदार्थ, नीचे दिए आरेख मे दर्शाये गए अनुसार, भरे गए हैं। यदि इन चारो परावैधुत पदार्थो के स्थान पर इस संधारित्र में K परावैधुतआंक का केवल एक परावैद्युतांक पदार्थ भरा जाये ताकि उसकी धारिता C ही हो, तो K का मान होगा

A

$\frac{1}{K} = \frac{1}{K_{1}} + \frac{1}{K_{2}} + \frac{1}{K_{3}} + \frac{3}{2 K_{4}}$

B

$K = K_{1} + K_{2} + K_{3} + 3 K_{4}$

C

$K = \frac{2}{3} (K_{1} + K_{2} + K_{3}) + 2 K_{4}$

D

$\frac{2}{K} = \frac{3}{K_{1} + K_{2} + K_{3}} + \frac{1}{K_{4}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

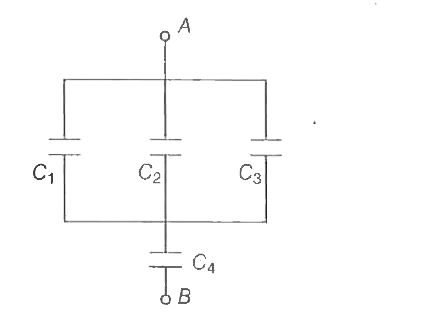
दिया है, सम्पूर्ण संधारित्र की धारिता C है।
अंत : $C = \frac{A ε_{0}}{d}$
(जहाँ,A = प्लेटो का क्षेत्रफल, d = प्लेटो के बीच की दूरी, $ε_{0}$ = निवार्त की विधुतशीलता)
$∴ C_{1} = \frac{2 ε_{0} K_{1} A}{3 d}, C_{2} = \frac{2 ε_{0} K_{2} A}{3 d}$ ,
$C_{3} = \frac{2 ε_{0} K_{3} A}{3 d}$ तथा $C_{4} = \frac{2 ε K_{4} A}{d}$
चित्रनुसार. $C_{1}, C_{2}$ व $C_{3}$ समांतर क्रम मे है।
अंत : तुल्य धारिता ,
$C . = C_{1} + C_{2} + C_{3} = \frac{2 ε_{0} A}{3 d} (K_{1} + K_{2} + K_{3})$
तथा $C_{4}$ श्रेणीक्रम में है।
$\frac{1}{C} . . = \frac{1}{C} . + \frac{1}{C_{4}} = \frac{3 d}{2 ε_{0} A (K_{1} + K_{2} + K_{3})} + \frac{d}{2 ε_{0} K_{4} A}$
अंत: प्रश्नशार $\frac{1}{C} = \frac{1}{C}$
$\Rightarrow \frac{d}{ε_{0} K A} = \frac{3 d}{2 ε_{0} A (K_{1} + K_{2} + K_{3})} + \frac{d}{2 ε_{0} K_{4} A}$
$\Rightarrow \frac{1}{K} = \frac{3}{2 (K_{1} + K_{2} + K_{3})} + \frac{1}{2 ε_{0} K_{4} A}$
$\Rightarrow \frac{2}{K} = \frac{3}{K_{1} + K_{2} + K_{3}} + \frac{1}{K_{4}}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

NEET PREVIOUS YEAR-स्थिर वैद्युत विभव तथा धारिता-MCQs

Home
Ask Doubt
Profile