In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar(△ABC)=ar(△ABD)
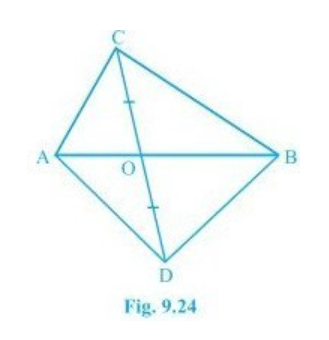
As CD is bisected by AB at O, it means,
AO is the median of triangle ACD and BO is the median of triangle BCD.
As median divides a triangle into two triangles with the same area.
ar(AOC)=ar(AOD) and ar(BOC)=ar(BOD)
So,ar(AOC)+ar(BOC)=ar(AOD)+ar(BOD)
ar(ABC)=ar(ABD)
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Solved Examples
4 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise 9.2
6 Videos
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - EXERCISE 10.2
2 Videos
Similar Questions
In Fig. 9.22, ABCD is a quadrilateral and BE ∣∣ ACand also BE meets DC produced at E. Show that area of ΔADEis equal to the area of the quadrilateral ABCD.
View SolutionABCD is a parallelogram, AE⊥DCand CF⊥AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
View SolutionRecall that two circles are congruent if they have the same radii. Prove that equalchords of congruent circles subtend equal angles at their centres.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionआकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज है यदि रेखाखड़ CD रेखाखड़ AB से बिंदु O पर समद्विभाजित होता है , तो दर्शाइए कि ar(ABC)=ar(ABD) है

View Solutionचित्र में AB आधार पर दो त्रिभुजों ABC तथा ABD है है यदि रेखाखण्ड CD को रेखा AB बिंदु O पर प्रतिच्छेद करती है, तो प्रदर्शित कीजिए कि ar(ΔABC)=ar(ΔABD)

View SolutionIn, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
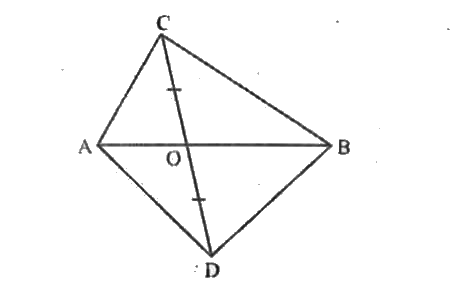
View SolutionIn the given figure, ABC and ABD are two triangles on the same base AB . If line - segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD)
View SolutionIn the figure, ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by ¯¯¯¯¯¯AB at O, show that ar (ΔABC)=ar(ΔABD).
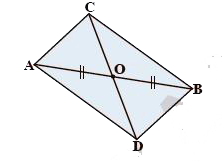
View Solution
