The sum of angles of elevation of the top of a tower from two points distance a and b from the base and in the same straight line with it is 90∘. Then the height of the tower is :Solution in Telugu
a2b
ab2
√ab
ab
The correct Answer is:C
Step by step video, text & image solution for The sum of angles of elevation of the top of a tower from two points distance a and b from the base and in the same straight line with it is 90^@. Then the height of the tower is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
10∑r=0(40−r)C5=
View SolutionLet α≠β satisfy α2+1=6α,β2+=6β. Then, the quadratic equation whose roots are αα+1,ββ+1 is
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
View SolutionThe angle of elevation of the top of a tower from two points on the ground at distances a metres and b metres from the base of the tower and in the same straight line are complementary.Prove that height of the tower is sqrt(ab).
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View SolutionIf the angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary, find the height of the tower.
View SolutionIf the angles of elevation of the top of a tower from two points at distances a and b from the base and in the same straight line with it are complementary then the height of the tower is
View Solutionयदि किसी मीनार के आधार से a तथा b (a>b) दूरी पर उसी सरल रेखा पर स्थित दो बिन्दुओं से मीनार के शिखर के उन्नयन कोण क्रमशः 30∘ तथा 60∘हैं, तो मीनार की ऊँचाई हैं :
View Solutionयदि किसी मीनार के आधार से और एक सरल रेखा में a तथा b दूरी पर स्थित दो बिन्दुओं से मीनार के शीर्ष के उन्नयन कोण पूरक हैं, तो मीनार की ऊँचाई हैं :
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4m and 9m, find the height of the tower from the base of the tower and in the same straight line with it are complementary.
View Solutionयदि किसी मीनार के आधार सेa तथा b(a>b) दूरी पर उसी सरल रेखा पर स्थित दो बिन्दुओ से मीनार के शिखर के उन्नयन किन क्रमशः 30∘ व 60∘ हो तो मीनार की ऊंचाई है -
View SolutionThe sum of angles of elevation of the top of a tower from two points distance a and b from the base and in the same straight line with it is 90∘. Then the height of the tower is :
View SolutionThe angles of elevation of e top of an inaccessible tower from two points on the same straight line from the base of the tower are 30∘and60∘, respectively. If the points are separated at a distance of 100 m, then the height of the tower is close to
View SolutionThe angle of elevation of the top of a tower of height "h" metres from two points at a distance of "a" and "b" metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab meters.
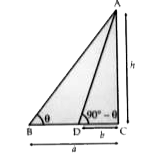
View SolutionThe angles of elevation of the top of a tower from two points at a distances a meter and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View SolutionIf the angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary, find the height of the tower.
View Solution
