Three uniform rods, each of length 2l and of the same mass are kept along three arms of a square in order. Find the position of the centre of gravity of the system.Solution in Bengali
at a distance of 2l3 from the second rod towards the centre of the square
Topper's Solved these Questions
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - Hots Numerical Problems ( Miscellaneous )
3 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - ENTRANCE CORNER ( Assertion-reason type )
5 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - Hots Numerical Problems ( Based on Equilibrium of Force )
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - CBSE Scanner
14 Videos
Similar Questions
A string passes over two smooth pulleys kept at a horizontal distance 2l. The two free ends of the string support two equal masses. From the middle of the string a third object of the same mass is suspended and released. How far would this mass descend vertically?
View SolutionThese questions have statement I and statement II. Of the four choices given below, choose the one that best describes the two statements.
Statement I: The centre of mass of the system will not alter in any direction if the external force is not exerted on it.
Statement II: If net external force is zero then the linear momentum of the system remains constant.
View SolutionA counterpoising 50-g weight is suspended from the ends of two strings of length 7 cm and 24 cm. The other ends of the strings are fixed rigidly at the two ends of a uniform rod of length 25 cm. If the weight and the midpoint of the rod remain in equilibrium on the same vertical line, find teh tension in the strings.
View SolutionExplain the relation in phase between displacement velocity and acceleration in SHM, graphically as well as theoretically.
View SolutionA progressive wave is given by y(x,l)=Bcos(300t−0.15x) where x and y are in cm and t in second . What is the (i) direction of propagation, (ii) wavelength , (iii) frequency, (iv) wave speed and (v) phase difference between two points 0 . 2 m apart ?
View SolutionFind the distance between centre of gravity and centre of mass of a two particle system attached to the ends of a light rod. Each particle has same mass. Length of the rod is R, where R is the radius of earth.
_E01_014_Q01.png)
View SolutionThree rods of the same mass are placed as shown in the figure. Calculate the coordinates of the centre of mass of the system.
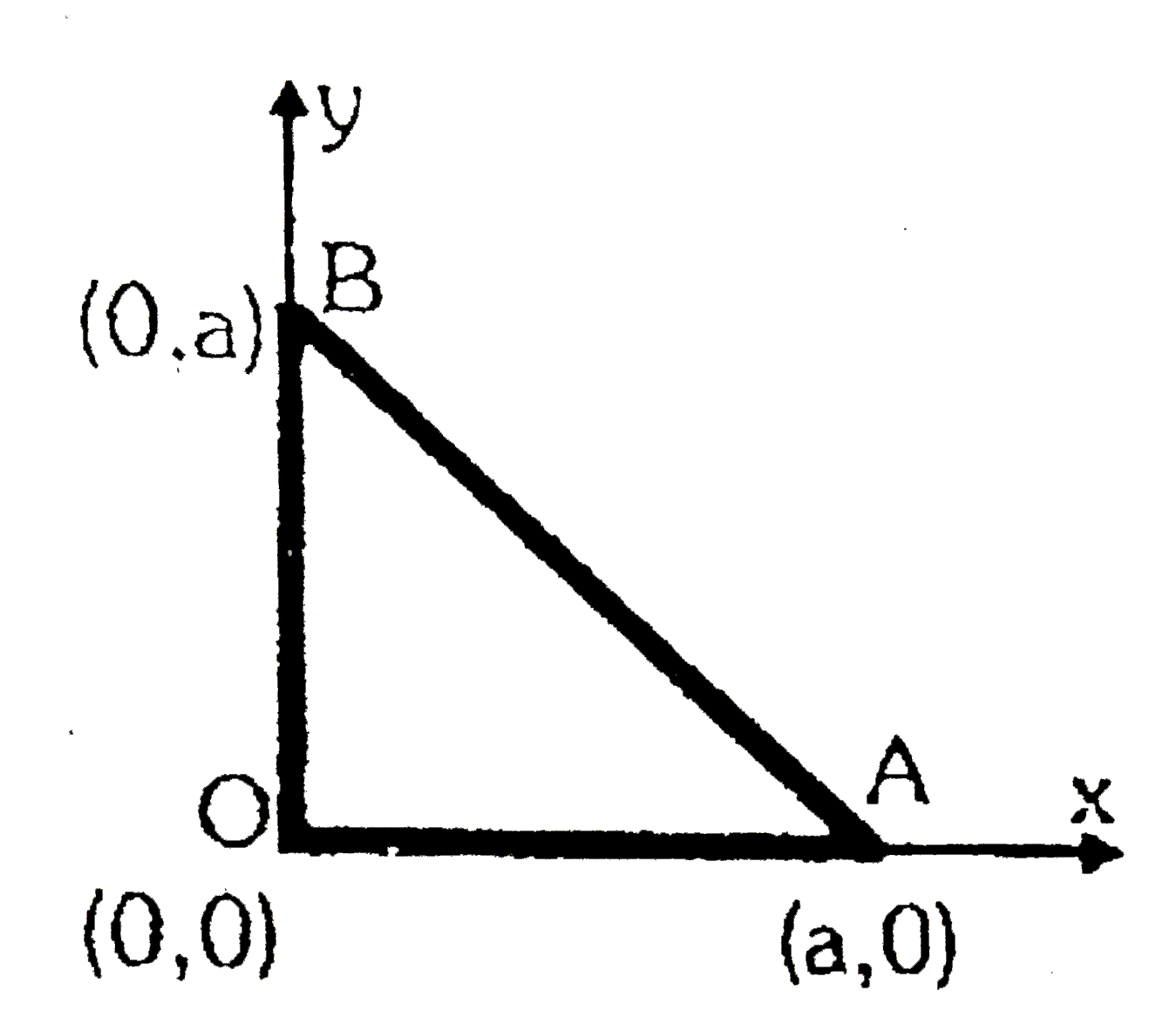
View SolutionThree uniform thin rods, each of mass 1 kg and length sqrt3 \ m, are placed along three co-ordinate axes with one end at the origin. The moment of inertia of the system about X-axis is
View SolutionThree thin uniform rods each of mass M and length L and placed along the three axis of a Cartesian coordinate system with one end of each rod at the origin. The M.I. of the system about z-axis is
View SolutionThe y co - ordinate of the centre of mass of the system of three rods of length 2a and two rods of length a as shown in the figure is (Assume all rods to be of uniform density)
View SolutionThree uniform discs each of mass .m. and radius .r. are kept touching each other, such that their centres form a triangle. The MI of the system about a median is
View SolutionThree thin uniform rods each of mass M and length L are placed along the three axes of a cartesian coordinate system. The moment of inertia of the system about z-axis is
View SolutionIf three rods of same mass are placed as shown in the figure, the co-ordinates of the centre of mass of the system are
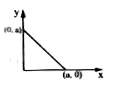
View SolutionThree uniform discs each of mass 'm' and radius 'r' are kept touching each other, such that their centres form a triangle. The M.I. of the system about a median of
View SolutionThree rods of the same mass are placed as shown in the figure. Calculate the coordinates of the centre of mass of the system.

View Solution
