Find the distance between centre of gravity and centre of mass of a two particle system attached to the ends of a light rod. Each particle has same mass. Length of the rod is R, where R is the radius of earth.
_E01_014_Q01.png)
R
R/2
zero
R/4
The correct Answer is:B
Centre of gravity of the two particles
XCG=W1X1+W2X2W1+W2=(0)(0)+(mg)(R)0+mg=R
the centre of mass of the two particle system is at
XCM=M(R)+m(0)2M=R2
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 2 (Brain Teasers)
27 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 3 (Miscellaneous Type Questions)
20 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
48 Videos
Similar Questions
Knowledge Check
The centre of mass of two particles system lies
Aat the midpoint on the line joining the two particles.Bat one end of line joining the two particlesCon the line perpendicular to the line joining two particlesDon the line joining the two particlesIf the mass of moon is M81, where M is the mass of earth, find the distance of the point where gravitational field due to earth and moon cancel each other, from the centre of moon. Given the distance between centres of earth and moon is 60 R where R is the radius of earth
A4 RB8 RC12 RD6 RStatement-1 : The centre of mass of a two particle system lies on the line joining the two particles, being closer to the heavier particle.
Statement-2 : Product of mass of one particle and its distance from centre of mass is numerically equal to product of mass of other particle and its distance from centre of mass.AStatement-1 is True, Statement-2 is True,
Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True,
Statement-2 is NOT a correct explanation for Statement-1CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is False
(i) A regular polygon has 2016 sides and r is the radius of the circle circumscribing the polygon. Particles of equal mass are placed at 2015 vertices of the polygon. Find the distance of the centre of mass of the particle system from the centre of the polygon.
(ii) In the last problem you have been asked to remove any one particle from the system so that the centre of mass of the remaining 2014 particles lies farthest from the geometrical centre of the polygon. Which particle will you remove ?
View SolutionFind the moment of inertia A of a spherical ball of mass m and radius r attached at the end of a straight rod of mass M and length l, if this system is free to rotate about an axis passing through the end of the rod (end of the rod opposite to sphere).

View SolutionFind the centre of gravity of a uniform vertical rod height = R/3, where R is the radius of Earth. The lower end of the rod is touching the surface of the Earth.
View SolutionThe y co - ordinate of the centre of mass of the system of three rods of length 2a and two rods of length a as shown in the figure is (Assume all rods to be of uniform density)
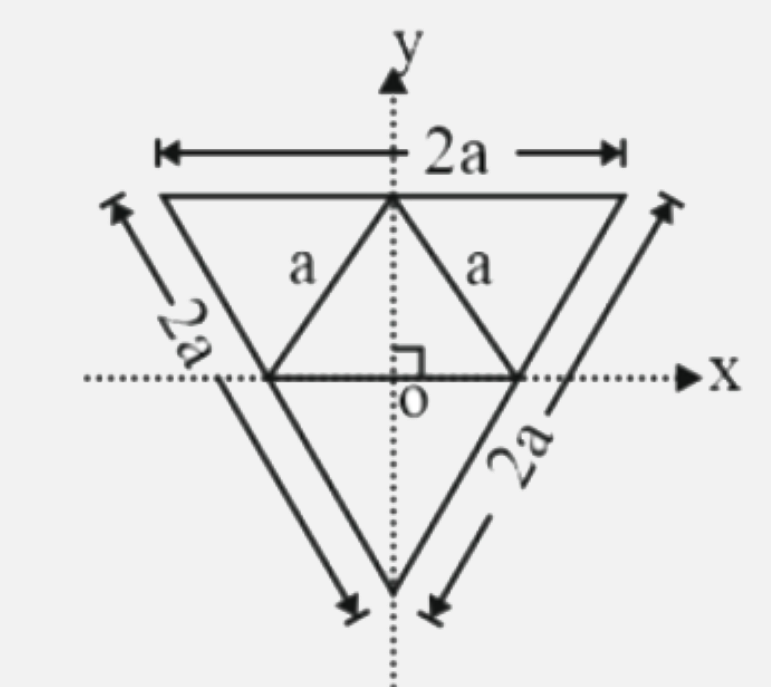
View SolutionFind the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
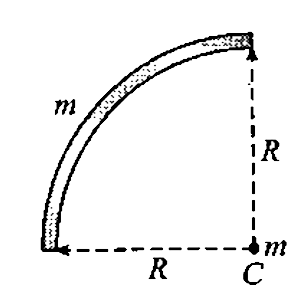
View Solution