A string passes through a hole at the centre of a horizontal table. The upper end of the string is tied to a mass m kept on the table, and at the lower end, a body of mass M is kept hanging. If the table rotates at an angular velocity ω, the mass M remains at rest. Show that, ω=√Mm⋅gr.
[ r is the radius of the circular path along which the mass m is rotating ] Solution in Bengali
Step by step video & image solution for A string passes through a hole at the centre of a horizontal table. The upper end of the string is tied to a mass m kept on the table, and at the lower end, a body of mass M is kept hanging. If the table rotates at an angular velocity omega, the mass M remains at rest. Show that, omega = sqrt((M)/(m)cdot(g)/(r)). [ r is the radius of the circular path along which the mass m is rotating ] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - ENTRANCE CORNER
5 Videos
- CIRCULAR MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - MULTIPLE CORRECT ANSWER TYPE
2 Videos
- CIRCULAR MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - PROBLEM SET - II
20 Videos
- CALORIMETRYBOOK - CHHAYA PUBLICATIONCHAPTER - CALORIMETRYEXERCISE - EXAMINATION ARCHIVE
5 Videos
- DOPPLER EFFECT IN SOUND BOOK - CHHAYA PUBLICATIONCHAPTER - DOPPLER EFFECT IN SOUND EXERCISE - CBSE SCANNER
2 Videos
Similar Questions
Statement I: If a car is taking a turn on a banked road, then the normal contact force between car and road is greater than the weight of car (neglecting friction).
Statement II: On a banked road, horizontal component of normal contact force between car and road provides necessary centripetal force. Assume friction is absent.
View SolutionIn uniform circular motion of a particle
View SolutionThe wheel of a car of radius 0.7 m is moving with an angular velocity of 10π rad⋅s−1. If the car is to be brought to rest by applying brakes within 12 s, what will be the distance covered by the car during that time?
View SolutionA 10 Watt electric heater is used to heat a container filled with 0.5 kg of water. It is found that the temperature of water and the container rises by 3, K in 15 minutes. The container is then emptied, dried and filled with 2 kg of oil. The same heater now raises the temperature of container-oil system by 2''K in 20 minutes. Assuming that there is no heat loss in the process and the specific heat of water as 4200 J . kg−1.K−1, the specific heat of oil in the same unit is equal to
View SolutionA train standing at the outer singal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 10 m/s, (b) recedes from the platform with a speed of 10 m/s. (ii) What is the speed of sound in each case if the speed of sound in still air is 340 m/s.
View SolutionA thread is passing through a hole at the centre of frictionless table. At the upper end a block of mass 0.5 kg is tied and a block of mass 8.0 kg is tied at the lower end which is freely hanging. The smaller mass is rotate, on the table with a constant angular velocity about the axis passing through the hole so as to balance the heavier mass. If the mass of the hanging block is changed from 8.0 kg to 1.0 kg , what is the fractional change in the radius and the angular velocity of the smaller mass so that it balances the hanging mass again?
View SolutionA body of mass m and radius r is rotated with angular velocity ω as shown in the figure & kept on a surface that has sufficient friction then the body will move

View SolutionA uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity ω about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
View SolutionA mass m rotating freely in a horizontal circle of a radius 1m on a frictionless smooth table support a stationary mass 2m, attached to the other end of the string passing through smooth hole O in table, hanging vertically. Find the angular velocity of rotation.
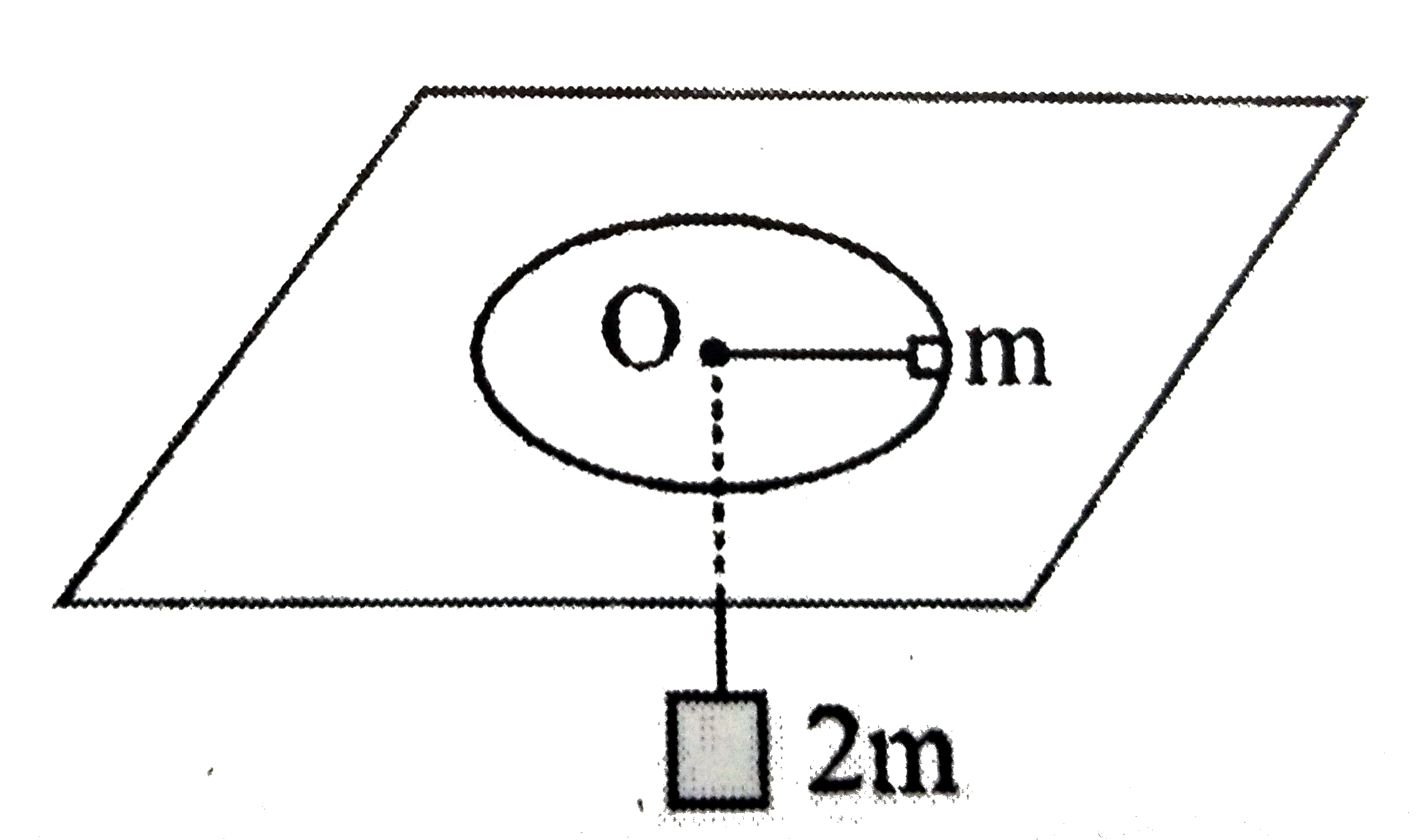
View SolutionA unifrom rod of mass m and length L is kept on a horizontal table with L4 length on the table. The end B is tied to a string as shown in the figure. The string attached to the end B is cut and the rod starts rotating about point C. Find the normal reaction from the table on the earth as soon as the string is cut.

View SolutionA mass m on a friction less table is attached to a hanging mass M by a cord through a hole in the table . Then the angular speed with which m must spin for M stay at rest will be
View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View SolutionA bock of mass M is on a horizontal table and is connected to an inextensible string. The string passes over a frictionless pulley fitted at one edge of the table. At the other end, another block of mass m hangs vertically. Coefficient fo friction between the table and the block of mass is mu . Find the acceleration of the system. Also find the tension in the string.
View SolutionA circular disc of mass m and radius r is rolling over a horizontal table top with angular velocity omega . Prove that the total energy of the disc , K = (3)/(4) m omega ^(2) r^(2) .
View SolutionA string is wound around a disc of radius r and mass M and at the free end of the string a body of mass m is suspended. The body is then allowed to descend. Show that the angular accelerationof the disc = mgR(M+m2)
View Solution
