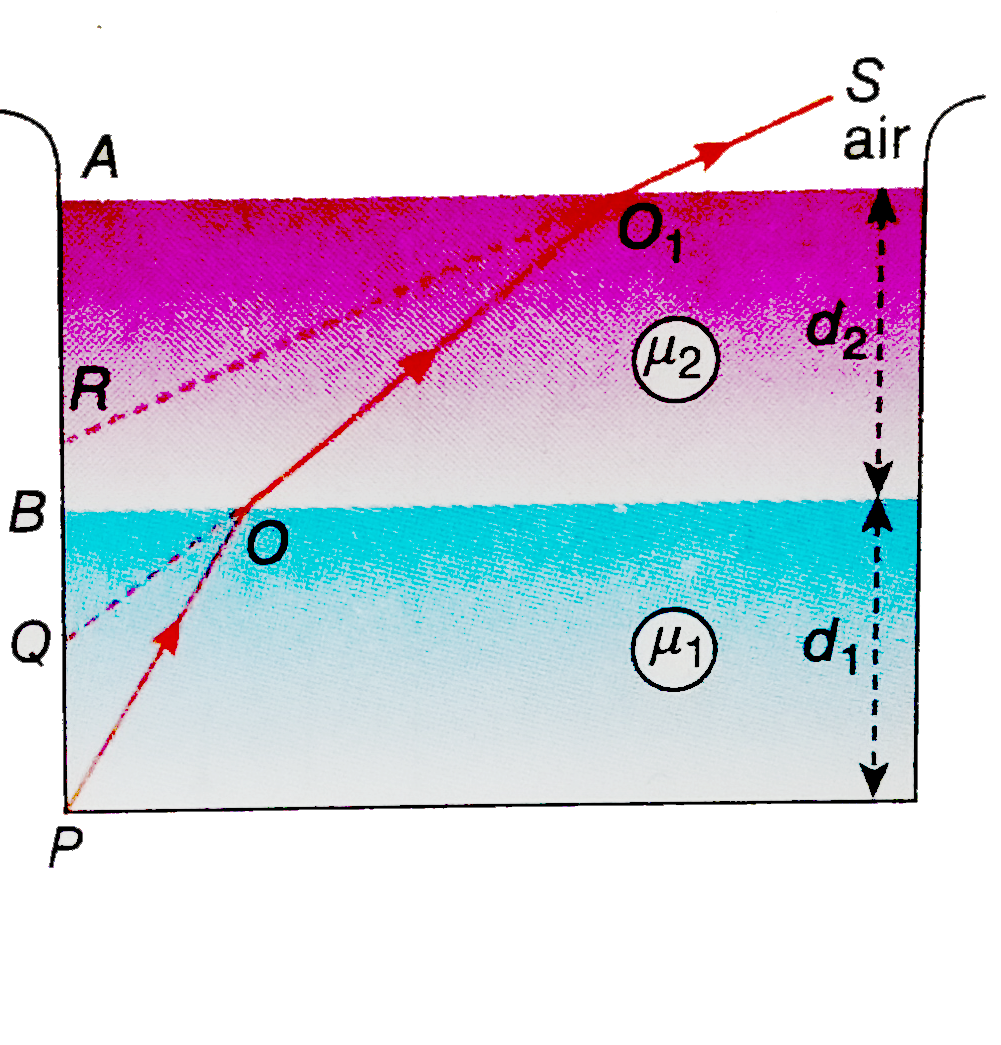
A vessel is filled with two mutually immiscible liquids of refractive indices $μ^{1} and μ^{2}$ . The depths of the two liquids are $d_{1} and d_{2}$ respectively. There is a mark at the bottom of the vessel. Show that the apparent depth of the mark when viewed normally is given by $(\frac{d_{1}}{μ_{1}} + \frac{d_{2}}{μ_{2}}) .$

Text Solution

Verified by Experts

The image of p is formed at Q due of refraction at the surface of separation B of the 1st and 2nd liquid. Another final image due to refraction in air from the second liquid is formed at R.
For the first refraction,
$\frac{μ_{1}}{μ_{2}} = \frac{B P}{B Q}$
$or, B Q = \frac{μ_{2}}{μ_{1}} . B P$
$\frac{μ_{1}}{μ_{2}} d_{1}$
For the second refraction,
$\frac{μ_{2}}{1} = \frac{A Q}{A R}$
$or, A R = \frac{A Q}{A R} = \frac{1}{μ_{2}} (A B + B Q)$
$or, A R = \frac{1}{μ_{2}} (d_{2} + \frac{μ_{2}}{μ_{1}} d_{1}) = \frac{d_{2}}{μ_{2}} + \frac{d_{1}}{μ_{1}}$
$∴$ Apparent depth of the mark P when viewed normally
$= A R = \frac{d_{1}}{μ_{1}} + \frac{d_{2}}{μ_{2}}$

Updated on:21/07/2023