A vessel is quarter filled with a liquid of refractive index μ. The remaining parts of the vessel is filled with an immiscible liquid of refractive index 3μ/2. The apparent depth of the vessel is 50% of the actual depth. The value of μ is
1.4
1.5
1.8
1.67
The correct Answer is:D
To solve the problem, we need to find the value of the refractive index μ for the liquid in the vessel. Let's break down the steps:
1. Understanding the Setup:
- The vessel is filled with two liquids. The first liquid has a refractive index μ and occupies 14 of the height H of the vessel. Therefore, the height of this liquid is H4.
- The second liquid has a refractive index 3μ2 and occupies the remaining 34 of the height of the vessel. Thus, the height of this liquid is 3H4.
2. Apparent Depth Calculation:
- The apparent depth da is given as 50% of the actual depth H. Therefore, we have:
da=H2
3. Using the Formula for Apparent Depth:
- The formula for the apparent depth when dealing with two different refractive indices is:
da=d1μ1+d2μ2
- Here, d1=H4 (depth of the first liquid) and d2=3H4 (depth of the second liquid).
- The refractive indices are μ1=μ and μ2=3μ2.
4. Substituting Values into the Formula:
- Substitute the known values into the formula:
H2=H4μ+3H43μ2
5. Simplifying the Equation:
- Simplifying the right-hand side:
H2=H4μ+2H4
- This simplifies to:
H2=H4μ+H2
6. Eliminating H:
- Since H is common in all terms, we can cancel it out (assuming H≠0):
12=14μ+12
7. Rearranging the Equation:
- Rearranging gives:
12−12=14μ
- This leads to:
0=14μ
- This is incorrect; we need to adjust our approach.
8. Correcting the Equation:
- Going back to:
H2=H4μ+3H8
- Multiply through by 8μ to eliminate the fractions:
4μ=2+3μ
9. Solving for μ:
- Rearranging gives:
4μ−3μ=2
μ=2
Final Answer:
The value of μ is 2.
- The vessel is filled with two liquids. The first liquid has a refractive index μ and occupies 14 of the height H of the vessel. Therefore, the height of this liquid is H4.
- The second liquid has a refractive index 3μ2 and occupies the remaining 34 of the height of the vessel. Thus, the height of this liquid is 3H4.
- The apparent depth da is given as 50% of the actual depth H. Therefore, we have:
da=H2
- The formula for the apparent depth when dealing with two different refractive indices is:
da=d1μ1+d2μ2
- Here, d1=H4 (depth of the first liquid) and d2=3H4 (depth of the second liquid).
- The refractive indices are μ1=μ and μ2=3μ2.
- Substitute the known values into the formula:
H2=H4μ+3H43μ2
- Simplifying the right-hand side:
H2=H4μ+2H4
- This simplifies to:
H2=H4μ+H2
- Since H is common in all terms, we can cancel it out (assuming H≠0):
12=14μ+12
- Rearranging gives:
12−12=14μ
- This leads to:
0=14μ
- This is incorrect; we need to adjust our approach.
- Going back to:
H2=H4μ+3H8
- Multiply through by 8μ to eliminate the fractions:
4μ=2+3μ
- Rearranging gives:
4μ−3μ=2
μ=2
The value of μ is 2.
Similar Questions
A vessel of depth 2d cm is half filled with a liquid of refractive index μ1 and the upper half with a liquid of refractive index μ2. The apparent depth of the vessel seen perpendicularly is
View SolutionA vessle of depth d is first filled to (23)rd of its depth with a liquid of refractive index 32 and the rest of the vessel is filled with a liquid of refractive index 43. What is the apparent depth of the inner surface of the bottom of the vessle.
View Solution
Knowledge Check
A vesse of depth x is half filled with oil of refractive index μ1 and the other half is filled with water of refrative index μ2. The apparent depth of the vessel when viewed above is
Ax(μ1+μ2)2μ1μ2Bxμ1μ22(μ1+μ2)Cxμ1μ2(μ1+μ2)D2x(μ1+μ2)μ1μ2
A vessle of depth d is first filled to (23)rd of its depth with a liquid of refractive index 32 and the rest of the vessel is filled with a liquid of refractive index 43. What is the apparent depth of the inner surface of the bottom of the vessle.
View SolutionA vessel of depth 2h is half filled with a liquid of refractive index 2√2 and the upper half with another liquid of refractive index √2. The liquids are immiscible. The apparent depth of the inner surface of the bottom of vessel will be:
View SolutionA lens of refractive index μ is put in a liquid of refractive index μ'. If focal length of lens in air is f, its focal length in liquid will be.
View SolutionA beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
View SolutionA prism of refractive index μg deviates the incident ray towards its base. If it is immersed in a transparent liquid of refractive index μ1 such that μ1>μg then prism would
View SolutionA thin lens made of a material of refractive index μ0 has a focal length f0 in air. Find the focal length of this lens if it is immersed in a liquid of refractive index μ.
View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
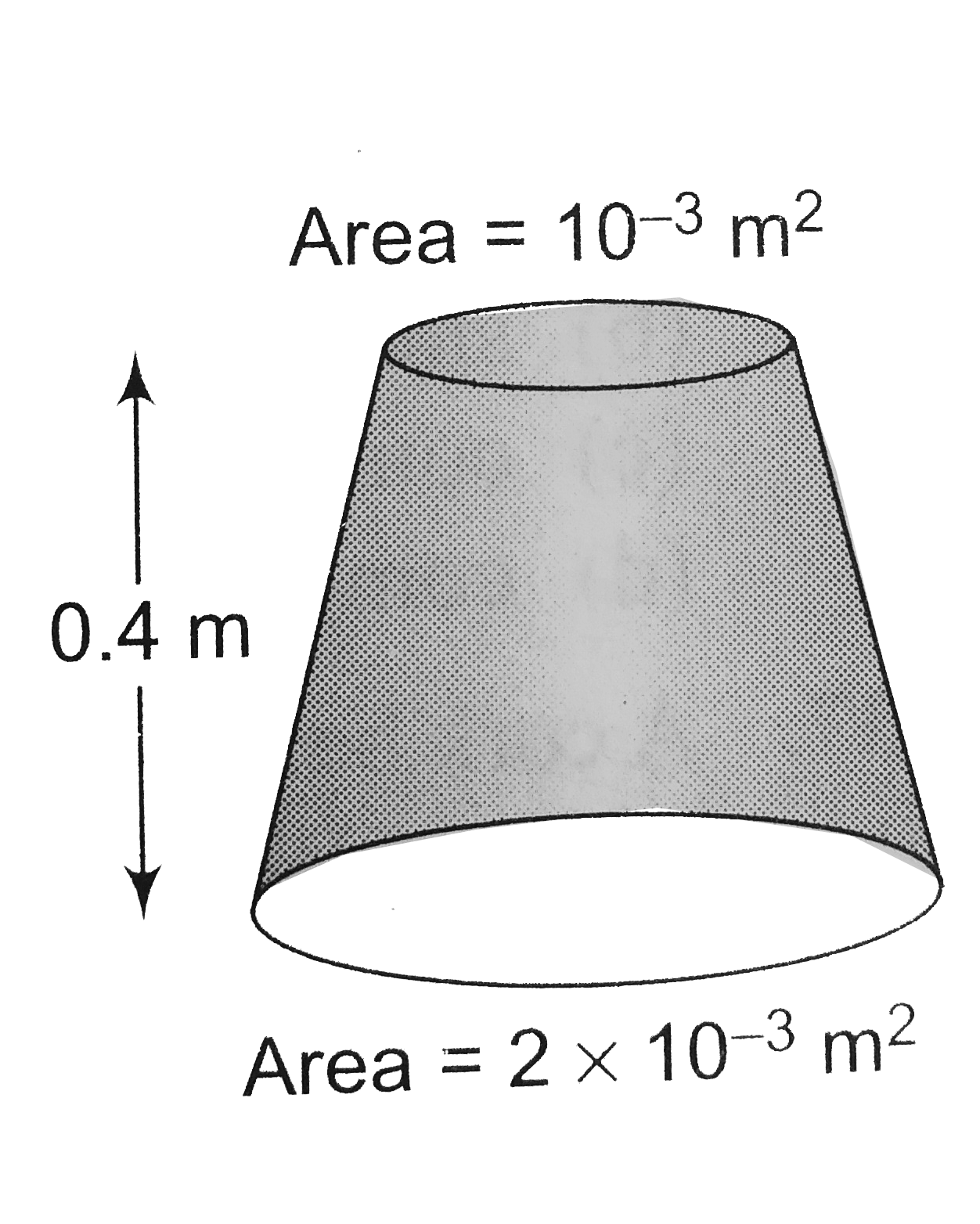
View Solution
