A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs touch. The centre of mass of the new disc is at a distance aR from the centre of the bigger disc. The value of a isSolution in Telugu
12
13
14
16
The correct Answer is:B
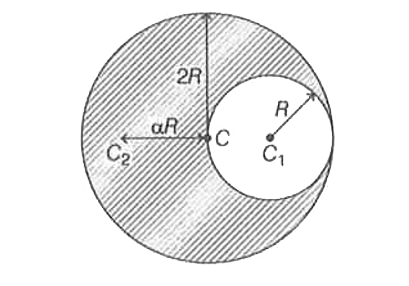
Let mass of entire disc = M
Mass per unit area = Mπ(2R)2=M4πR2
Mass of removed disc of radius R ,
M1=M4πR2×R2=M4
Mass of remaining disc
⇒M2=M−M4=3M4
Center of mass of removed disc is C1 and centre of mass of remaining new disc is C2 And centre of mass of combination of M1 and M2 will be at C(0,0).
⇒M1x1−M2−x2M1−M2=0
⇒M1x1=M2x2
M4.R=3M4(αR) ⇒α=13
Topper's Solved these Questions
Similar Questions
A car moving with a certain velocity jumps form an inclined plane placed at one bank of a river and reaches the other bank by attained a maximum height of 80 m if the same car moving with the same velocity jumps from another inclinded plane having different angle of inclination and reaches the same point on the other bank by attaining maxmimum height of 45 m then the width of the river is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is αR from the center of the bigger disc. The value of α is
View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at

View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2 R such that the circumferences of the discs coincide. The center of mass of new disc is alpha R from the center of the bigger disc. The value of alpha is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs touch. The centre of mass of the new disc is at a distance aR from the centre of the bigger disc. The value of a is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R, such that the circumference of the disc coincides. The centre of mass of the new disc is αR from the centre of bigger disc. The value of alpha is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is alphaR from the centre of the bigger disc . the value of alpha is
View SolutionA circular disc of radius R is removed from a bigger circular dise of radius such that the circumferences of the discs coincide. The centre of mass of the new disc is alphaR from the centre of the bigger disc. The value of a is:
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the disc coincide. The centre of mass of the new disc is αR from the centre of the bigger disc. The value of α is :
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs touch. The centre of mass of the new disc is at a distance aR from the centre of the bigger disc. The value of a is
View SolutionA circular disc of radius R is removed from a bigger of the discs coincide. The centre of mass of the new disc is ar from the centre of the bigger disc. The value of α is
View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at

View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.

View SolutionThe distance of center of mass from the center of a uniform disc of radius R. if a circular plate is removed from the disc as shown in figure will be (C is centre of complete disc)
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2 R such that the circumferences of the discs coincide. The center of mass of new disc is alpha R from the center of the bigger disc. The value of alpha is
View Solution

