The moment of inertia of a body about a given axis is 12kg.m2. Initially, the body is at rest. In order to produce a rotational kinetic energy of 15000J, an angular acceleration of 10rads−2 must be applied about that axis for a duration of Solution in Telugu
2s
4s
10s
5s
The correct Answer is:D
Given, moment of inertia, I=12kg−m2
Rotational kinetic energy, Ek=12Iω2
15000J=12×12×ω2
So, ω=√3000012=√2500=50 rad/s
Angular acceleration, α=10rad/s2
As α=ωt
So, time =ωα=5010=5s
Topper's Solved these Questions
- AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)EXERCISE - Physics
40 Videos
- AP EAMCET SOLVED PAPER 2019BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET SOLVED PAPER 2019EXERCISE - PHYSICS
40 Videos
Similar Questions
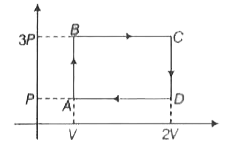
A monoatomic ideal gas through a cyclic process as shown in the figure . The efficiency of this process is
View SolutionTwo intervals of time are measured as Δt1=(2.00±0.02)sandΔt2(4.00±0.02)s. The value of √(Δt1)(Δt2) with correct significant figures and error is
View SolutionThe moment of inertia of a body about a given axis is 1.2kgm2. Initially, the body is at rest. In order to produce a rotational KE of 1500j, for how much duration, an acceleration of 25rads−2 must be applied about that axis ?
View SolutionThe moment of inertia of a body about a given axis is 1.2kgm2. Initially, the body is at rest. In order to produce a rotational KE of 1500J, for how much duration, an acceleration of 25rads−2 must be applied about that axis ?
View SolutionThe moment of inertia of the body about an axis is 1.2 kg m^(2) . Initially the body is at rest. In order to produce a rotational kinetic energy of 1500J, an angualr acceleration of 25 rad/s^(2) must be applied about the axis for the duration of
View SolutionThe moment of inertia of a body about a given axis is 3.6 kg m2. Initially, the body is at rest. In order to produce a rotational K.E. of 800 J, an acceleration of 15 rad s must be applied about that axis for
View SolutionMoment of inertia of a body about a given axis is 1.5 kg m^(2) . Initially the body is at rest. In order to produce a rotational kinetic energy of 1200 J, the angular acceleration of 20 rad//s^(2) must be applied about the axis for a duration of _________ (in sec).
View SolutionMoment of inertia of a body about a given axis is 1.5kgm2. Intially the body is at rest. In order to produce a rotational kinetic energy iof 1200 J, the angular acceleration of 20 rad/s2 must be applied about the axis for a duration of
View SolutionThe M.I. of a body is 1.2 kg m2. Initially the body is at rest. In order to produce a rotational kinetic energy of 1500 J an angular acceleration of 25 rad s−2 must be applied about the axis for a duration of
View SolutionThe moment of inertia of a body about a given axis is 1.2 kg m^2 . Initially, the body is at rest. In order to produce a rotational kinetic energy of 6000 joule, an angular acceleration of 25 rad/ s^2 must be applied about that axis for a duration of
View SolutionThe moment of inertia of a body about a given axis is 1.2 kg m2. · Initially, the body is at rest. In order to produce a rotational kinetic energy of 1500 J, an angular acceleration of 25 rad/s2 must be applied about that axis for a duration of
View SolutionThe moment of inertia of a body about a given axis is 2.4kg–m2. To produce a rotational kinetic energy of 750 J, an angular acceleration of 5 rad/s2 must be applied about that axis for
View SolutionThe M.I. of a body is 1.2kgm^(2) . Initially the body is at rest. In order to produce a rotational kinetic energy of 1500J an angular acceleration of 25rads^(-2) must be applied about the axis for a duration of
View SolutionThe M.I. of a body is 1.2 kg m2. Initially the body is at rest. In order to produce a rotational kinetic energy of 1500 J an angular acceleration of 25 rad s−2 must be applied about the axis for a duration os
View SolutionThe M.I. of a body is 1.2" kg m"^(2) . Initially the body is rest. In order to produce a rotational kinetic energy of 1500 J an angular acceleration of 25" rad s"^(-2) must be applied about the axis for a duration of
View Solution
