A diamtomic gas consisting of rigid molecules is at a temperature of 87∘C. If the moment of inertia is 2.76×10−39gcm2, then the rms angular speed of the molecule is (Boltzmann constant =1.38×10−23JK−1)Solution in Telugu
6×1012rads−1
3×1012rads−1
6×1013rads−1
3×1013rads−1
The correct Answer is:A
Moment of inertia of diatomic molecule,
I=23Mr2
So, radius, r=√3I2M…(i)
rms speed of molecule,
v=√3kTM rms angular speed,
ω=vr=√3kT/M√3I/2M=√2kTI
=√2×1.38×10−23×(87+273)2.76×10−46
=√360×1023=√36×1024
=6×1012rad/s
Topper's Solved these Questions
- AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)EXERCISE - Physics
40 Videos
- AP EAMCET SOLVED PAPER 2019BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET SOLVED PAPER 2019EXERCISE - PHYSICS
40 Videos
Similar Questions
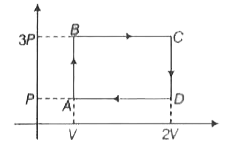
A monoatomic ideal gas through a cyclic process as shown in the figure . The efficiency of this process is
View SolutionTwo intervals of time are measured as Δt1=(2.00±0.02)sandΔt2(4.00±0.02)s. The value of √(Δt1)(Δt2) with correct significant figures and error is
View SolutionThe temperature of a gas consisting of rigid diatomic moleculoes is T = 300 K. Calculate the angular root-mean square velocity of a rotating molecules if its moment of inertia is I = 2.0 xx 10^(-40) kg m^(2) .
View SolutionEstimate the average thermal energy of a helium atom at (i) room temperature (27∘C). Boltzmann constant =1.38×10−23JK−1
View SolutionThe diameter of a gas molecule is 2.4×10−10m. Calculate the mean free path at NTP. Given Boltzmann constant k=1.38×10−23Jmo≤ce–−1K−1.
View SolutionThe average translational kinetic energy of nitrogen gas molecule is 0.02eV(1eV−1.6×10−19J). Calculate the temperatuire of the gas. Boltzmann constant k=1.38×10−23J/K.
View Solution0∘C पर किसी गैस के अणु की औसत गतिज ऊर्जा ज्ञात करो | यदि बोल्ट्जमैन स्थिरांक k=1.38×10−23 जूल/अणु K | क्या यह गैसीय अणु की प्रकृति पर भी निर्भर है |
View SolutionIf the average translational kinetic energy of a molecule in a gas is equal to the kinetic energy, of an electron accelerating from rest through 10 Volt, then the temperature of the gas molecule is (Boltzmann constant =1.38×10−23JK−1)
View SolutionIf the average translational kinetic energy of molecule in a gas is equal to the kinetic energy of an electron acceleration from rest through 10 V , then the temperature of the gas molecule is
(Boltzmann constant =1.38×10−23JK−1 )
View SolutionAt a temperature of 314 K and a pressure of 100 kPa , the speed of sound in a gas is 1380 ms^(-1) . The radius of each gas molecule is 0.5 Å . The frequency of sound at which the wavelength of sound wave in the gas becomes equal to the mean free path of the gas molecules is ( Boltzmann constant = 1.38 xx 10^(-23) JK^(-1) . )
View SolutionCalculate the translational kinetic energy and net kinetic energy of an oxygen molecule at 27^@C , where Avogadro number , N=6.023 times 10^23 and Boltzmann constant k= 1.38 times 10^-23 J.K^-1
View SolutionAt what temperature will the rms speed of oxygen molecules become just sufficient for escaping from the Earth's atmosphere? (Mass of oxygen molecules (m)=2.76×10−26 kg Boltzmann's constant (kB)=1.38×10−23JK−1)
View SolutionAt what temperature will the rms speed of oxygen molecules become just sufficient for escaping from the Earth's atmosphere ? (Given : Mass of oxygen molecule (m) = 2.76 xx 10^(-26) kg , Boltzmann's constant k_B = 1.38 xx 10^(-23) JK^(-1) )
View SolutionA gas molecule at the surface of earth happens to have the rms speed for the gas at 0∘C . Suppose it went straight up without colliding with other molecules, how high it would rise? Mass of the molecule is 4.65×10−26kg. Boltzmann's constant =1.38×10−23JK−1.
View SolutionThe temperature of a gas consisting of rigid diatomic moleculoes is T = 300 K. Calculate the angular root-mean square velocity of a rotating molecules if its moment of inertia is I=2.0×10−40kgm2.
View Solution
