A uniform horizontal rod of length l is dropped from height H above th two fixed edge shown in the diagram. If coefficient of restitution between the rod and fixed edges are $\frac{1}{2}$ and $\frac{1}{3}$ then find direction of angular velocity of the rod about it's centre of mass after the impact.

A

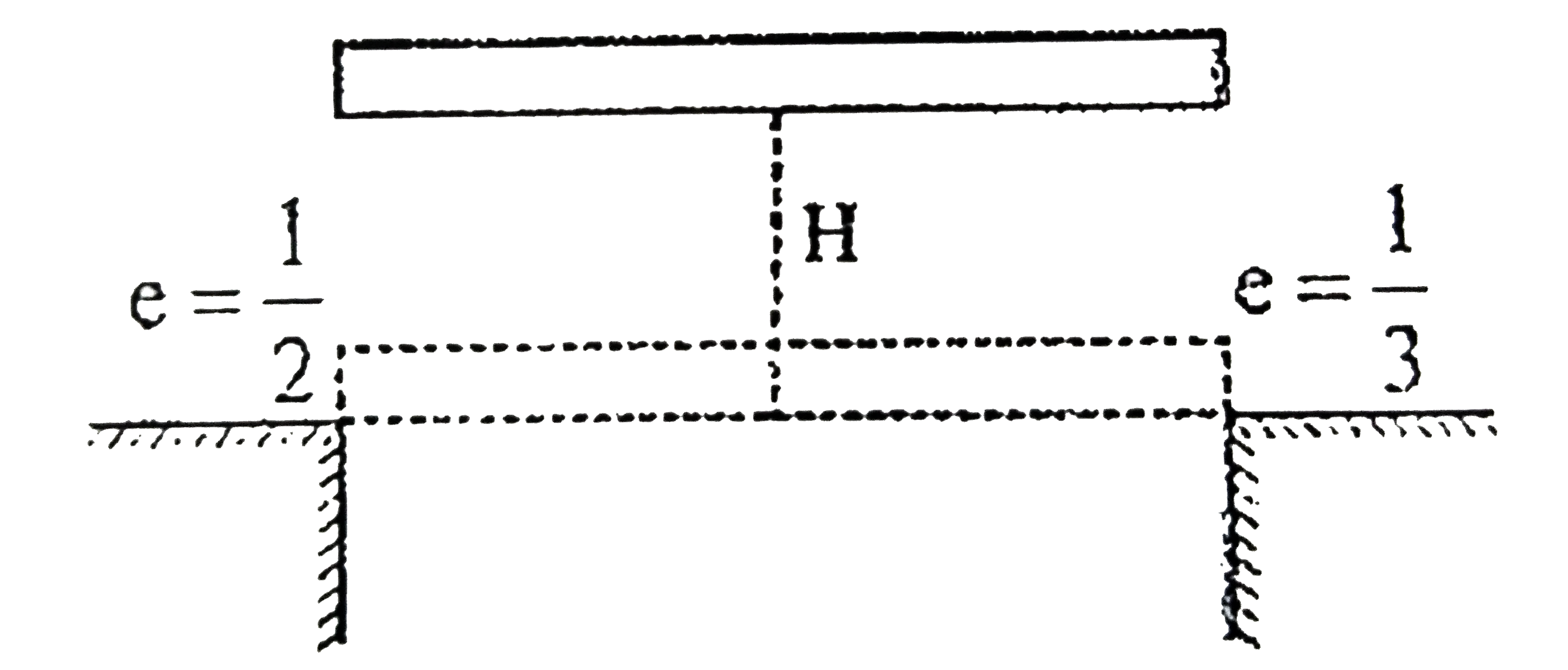
Clockwise

B

Anticlockwise

C

No rotation

D

Can not be determined

Video Solution

Text Solution

Verified by Experts

Velocity of seperation at left end must be high.

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A uniform horizontal rod of length l falls vertically from height h on two identical blocks placed symmertrically below the rod as shown in figure the coefficients of restitution are $e_{1}$ and $e_{2}$ the maximum height through which the centre of mass of the rod will rise after after bouncing off the blocks is

A $\frac{h}{(e_{1} + e_{2})}$
B $\frac{{(e_{1} + e_{2})}_{1}^{2} h}{4}$
C $\frac{{(e_{1} + e_{2})}_{1}^{2} h}{2}$
D $\frac{4 h}{(e_{1}^{2} + e_{2}^{2})}$
Question 2 - Select One
A rod $A B$ of length $1 m$ is placed at the edge for a smooth table as shown in figure. It is hit horizontally at point $B$ . If the displacement of centre of mass $m$ in $1 s$ is $5 \sqrt{2} m$ . The angular velocity of the rod is $(g = 10 m / s^{2})$

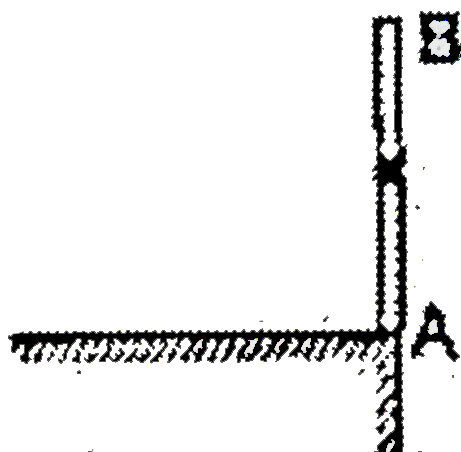A $30 r a d / s$
B $20 r a d / s$
C $10 r a d / s$
D $5 r a d / s$
Question 3 - Select One
A uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is $m l^{2} / 3$ , the initial angular acceleration of the rod will be

A $\frac{m g l}{2}$
B $\frac{3}{2} g l$
C $\frac{3 g}{2 l}$
D $\frac{2 g}{3 l}$

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile