Find the values of x∈[0,2π] for which function f(x)=tan−1(tanx)andg(x)=cos−1(cosx) are identical
Video Solution
Text Solution
The correct Answer is:[0,π/2)∪{2π]
Let us draw the graph of both th efunction for x∈[0,2π]
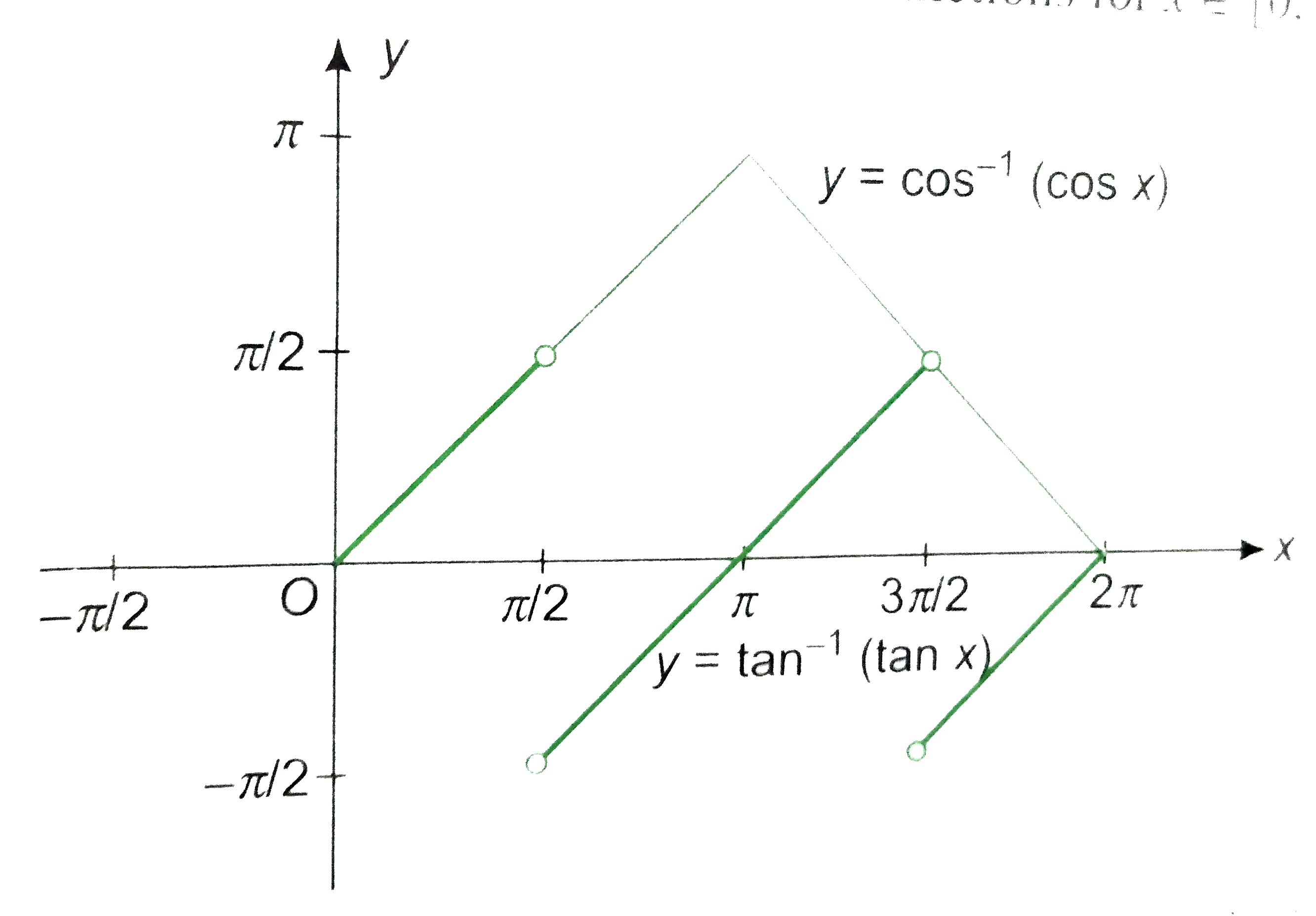
In the above figure, graph of y=f(x)andy=g(x) coincide for x∈[0,π/2)∪{2π}
|
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.3
12 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.4
12 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.1
12 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year
20 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
Similar Questions
Knowledge Check
The domain set of the function
f(x)=tan−1x−cot−1x+cos−1(2−x) isA[0,1]B[-1,1]C[1,3]DNone of theseLet the function f(x)=tan1−(sinx+cosx) be defined on [ 0, 2 pi] Then f(x) is
Aincreasing on [0,π/4)∪[5π4,2π]Bdecreasing on (Π/4,2π)Cincreasing on (0,π/4,)∪(3π/4,2π)Ddecreasing on [π/4,7π/4]
Find the value of x for which function are identical. f(x)=cosxandg(x)=1√1+tan2x
View SolutionFind the number of critical points of the function
f (x) = min (tan x , cos x) , x∈(0,π)
View SolutionFind period of the function f(x)=cos(tanx+cotx)cos(tanx−cotx)
View SolutionFind the value of x for which the function f(x)=1+2sinx+3cos2x(0≤x≤2π3)) is maximum. Also find these values of the function.
View SolutionFind the values of x for which the following pair of functions are identical.
(i) f(x)=tan−1x+cot−1x and g(x)=sin−1x+cos−1x
(ii) f(x)=cos(cos−1x) and g(x)=cos−1(cosx)
View SolutionFind the maximum and minimum values of the function f(x)=sinx1+tanx,(0<x<2π).
View Solution
