Find the area bounded by ysin−1(sinx) and x-axis for x∈[0,100π]
Video Solution
Text Solution
ysin−1(sinx) is periodic with period 2π
∴ Required area =50× (area bounded by y=sin−1(sinx) and x a-axis for x∈[0,2π])
Graph of y=sin−1(sinx) for x∈[0,2π] is as shown in the following figure.
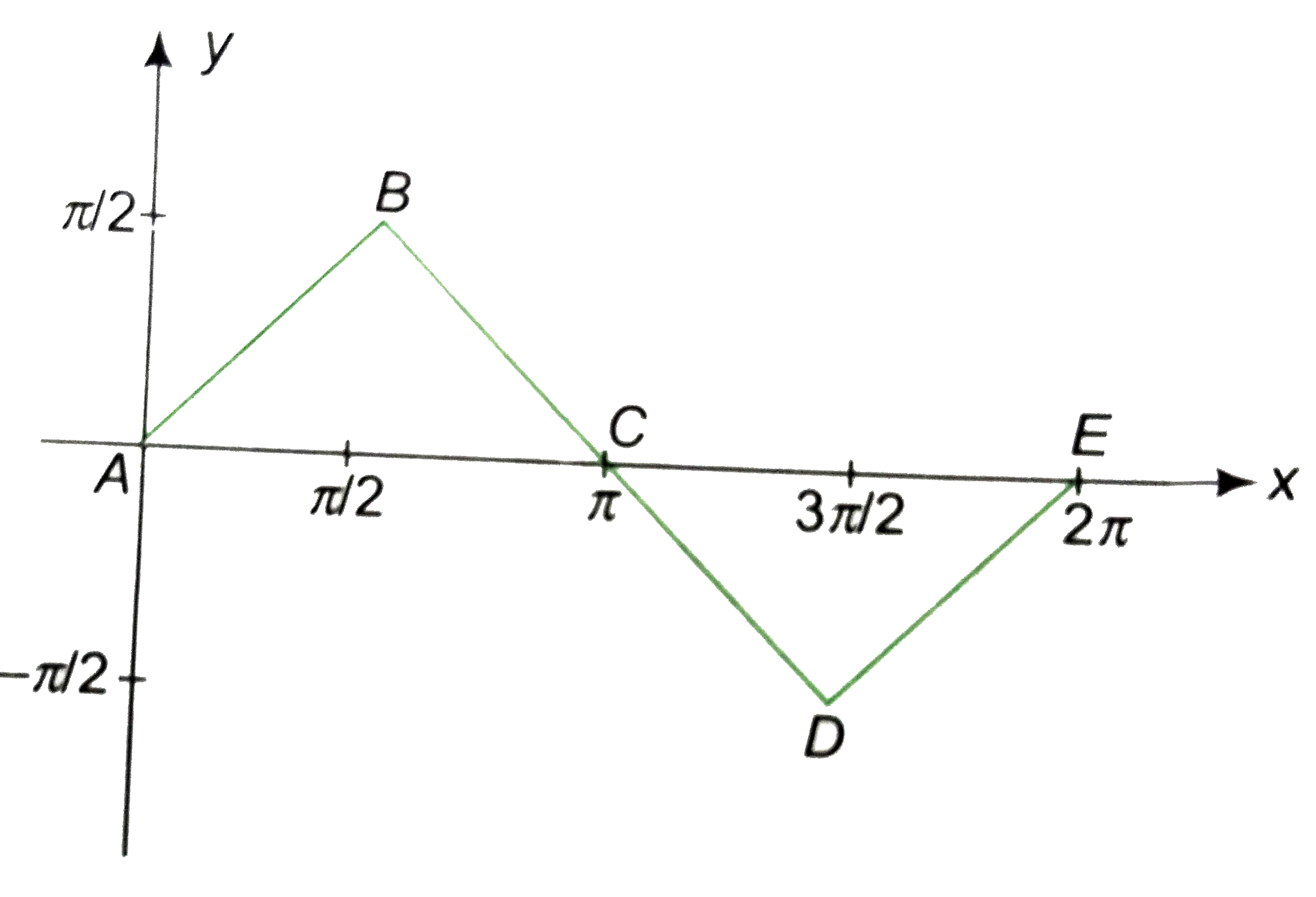
Required area =50×( area of ΔABC+area of ΔCDE)
=100×(area of ΔABC)
=100×(12×π×π2)
25π2
|
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.1
12 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.2
6 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year
20 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
Similar Questions
Knowledge Check
The area bounded by y=sin−1x,x=1√2 and X-axis is
A(1√2+1) sq unitsB(1−1√2) sq unitsCπ4√2 sq unitsD(π4√2+1√2−1) sq unitsThe area bounded by the curve y=sin2x−2sinx and the x-axis, where x∈[0,2π], is
A4 sq. unitsB8 sq. unitsC16 sq. unitsD20 sq. unitsThe area bounded by y=sin−1x, y-axis and |y|=π2 is
A2BπC2πD1
Find the area bounded by y = sin x and axis of x in (0,π)
View SolutionFind the area bounded by y=sin−1x,y=cos−1x,andthex−aξs.
View SolutionFind the area bounded by y=1+2sin2x,X-axis,X=0 and x=π.
View SolutionThe area bounded by y=x|sinx| and x - axis between x=0,x=2π is
View SolutionThe area bounded by y=sinx with y -axis for x in[−π2,π2] is
View Solution
