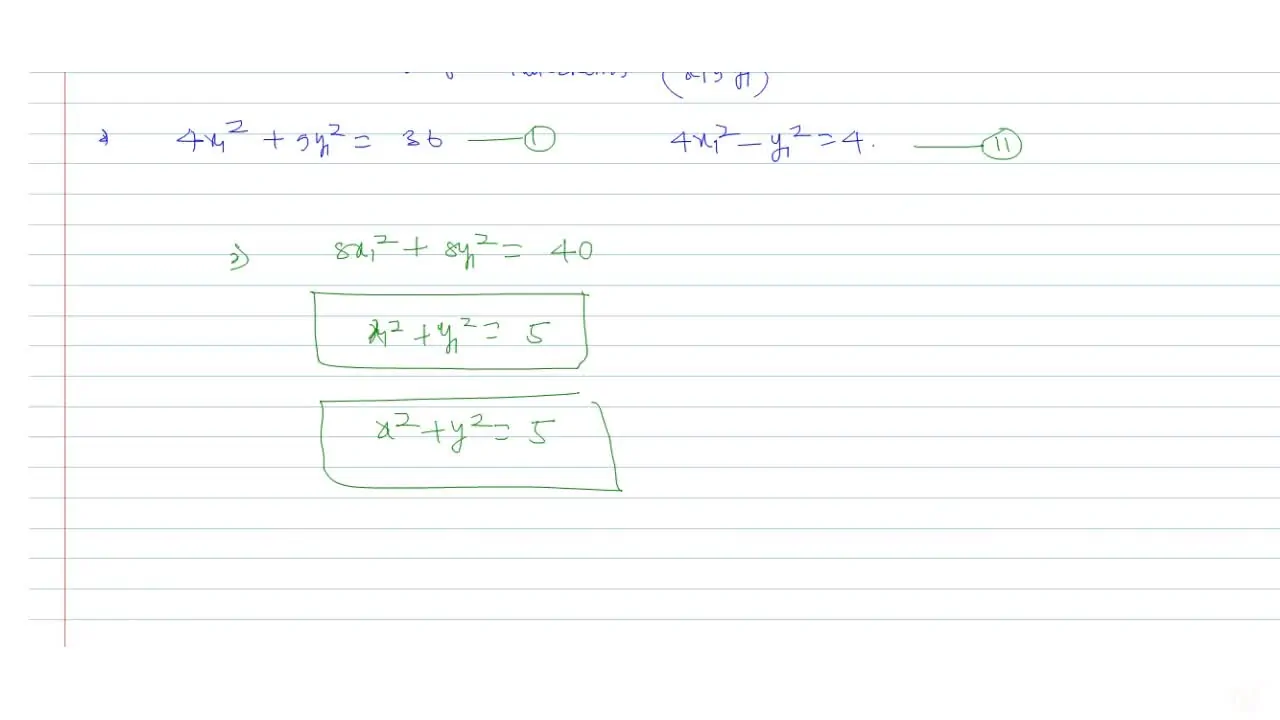The ellipse 4x2+9y2=36 and the hyperbola a2x2−y2=4 intersect at right angles. Then the equation of the circle through the points of intersection of two conics is x2+y2=5 √5(x2+y2)−3x−4y=0 √5(x2+y2)+3x+4y=0 x2+y2=25
x2+y2=5
√5(x2+y2)−3x−4y=0
√5(x2+y2)+3x+4y=0
x2+y2=25
The correct Answer is:A

Since ellipse and hyperbola intersect orthohonally, they are confocal.
Hence, a= 2 (equating foci).
Let the point of intersection in the first quadrant be P(x1,y1).
P lies on both the curves. Therefore,
4x21+9y21=36and4x21−y21=4
Adding these two results, we get
8(x21+y21)=40
or x21+y21=5
or r=√5
Hence, the equation of the circle is
x2+y2=5
Related Playlists
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise (Multiple)18videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise (Comprehension)21videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise 7.64videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year3videos
HIGHT AND DISTANCE
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Question Bank25videos
INDEFINITE INTEGRATION
Similar Questions
The ellipse 4x2+9y2=36 and the hyperbola a2x2−y2=4 intersect at right angles. Then the equation of the circle through the points of intersection of two conics is
View SolutionThe ellipse 4x2+9y2=36 and the hyperbola 4x2–y2=4 have the same foci and they intersect at right angles then the equation of the circle through the points of intersection of two conics is
View SolutionThe equation of the line through the intersection of the lines 2x−3y=0 and 4x−5y=2 and
 View Solution
View SolutionFind the equations of the straight lines joining the origin to the points of intersection of x2+y2−4x−2y=0 and x2+y2−2x−4y=4 .
View SolutionThe equation of the circle through the points of intersection of x y -1 -0, x y -2x-4 y l 0 and touching the line x 2y 0, is (B) x y 2 x+20 (C) x y (D) 2 (x2 y x 2
View SolutionFind the equation of the circle passing through the point of intersection of the circles x2+y2−6x+2y+4=0,x2+y2+2x−4y−6=0 and with its centre on the line y=x.
View SolutionThe equation of the circle through points of intersection of the circle x2+y2−4y+4=0 and the line x+2y=4 which touches the line x+2y=0, is
View SolutionThe equation of the line passing through the intersection of the circles 3x2+3y2−2x+12y−9=0 and x2+y2+6x+2y−15=0 is
View SolutionTwo circle x2+y2=6 and x2+y2−6x+8=0 are given. Then the equation of the circle through their points of intersection and the point (1, 1) is x2+y2−6x+4=0 x2+y2−3x+1=0 x2+y2−4y+2=0 none of these
View SolutionFind the point of intersection of the circle x2+y2−3x−4y+2=0 with the x-axis.
View Solution