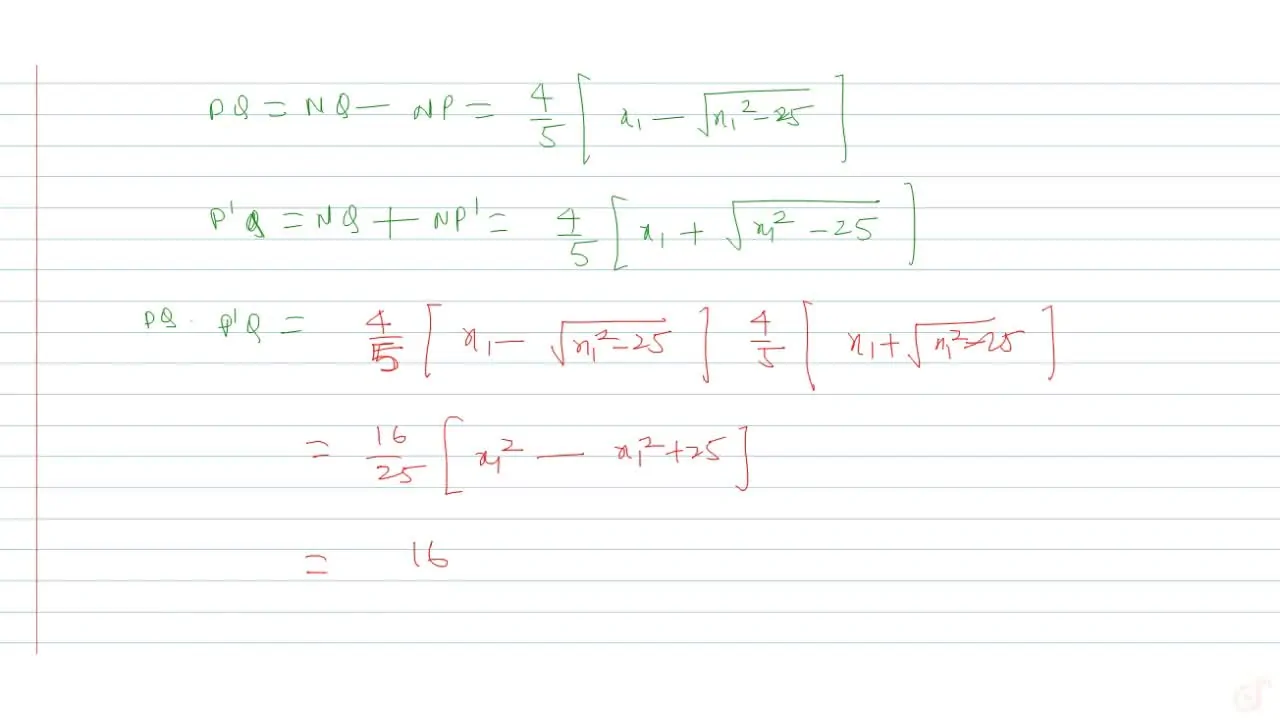Let any double ordinate PNP' of the hyperbola x225−y216=1 be produced on both sides to meet the asymptotes in QandQ' . Then PQ.P′Q is equal to 25 (b) 16 (c) 41 (d) none of these
25
16
41
none of these
The correct Answer is:B
NP=45√x21−25
Point Q is on
y=45x
NQ=45x1
PQ=NQ−NP
=45(x1−√x21−25)
P'Q=45(x1+√x21−25)
PQ⋅P'Q=16

Related Playlists
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise (Multiple)18videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise (Comprehension)21videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise 7.64videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year3videos
HIGHT AND DISTANCE
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Question Bank25videos
INDEFINITE INTEGRATION
Similar Questions
Let any double ordinate PNP' of the hyperbola x225−y216=1 be produced on both sides to meet the asymptotes in QandQ' . Then PQ.P′Q is equal to 25 (b) 16 (c) 41 (d) none of these
View SolutionLet any double ordinate PNP of the hyperbola x225−y216=1 be produced both sides to meet the asymptotes in Q and Q, then PQ.P1Q is equal to
View SolutionLet any double ordinate PNP1 of the hyperbol x29−y24=1 be produced both sides to meet the asymptotes in Q and Q', then PQ.P'Q is equal to
View SolutionLet the couble ordinate pp' of the hyperbola x24−y23=1 is produced both sides to meet asymptotes of hyperbola in Q and Q'. The product (PQ)(PQ)' is equal to :
View SolutionAsymptotes of a hyperbola x225−y216=1 are
View SolutionThe eccentricity of the hyperbola x225−y216=1 is
View SolutionThe tangent at P on the hyperbola x2a2−y2b2=1 meets one of the asymptote in Q. Then the locus of the mid-point of PQ is
View SolutionThe eccenttricity of the hyperbola x216−y225=1is
View SolutionThe ordinate of any point P on the hyperbola, given by 25x2−16y2=400, is produced to cut its asymptotes in the points Q and R. Prove that QP.PR=25.
View SolutionA straight line intersects the same branch of the hyperbola x2a2−y2b2=1 in P1 and P2 and meets its asymptotes in Q1 and Q2. Then, P1Q2−P2Q1is equal to
View Solution