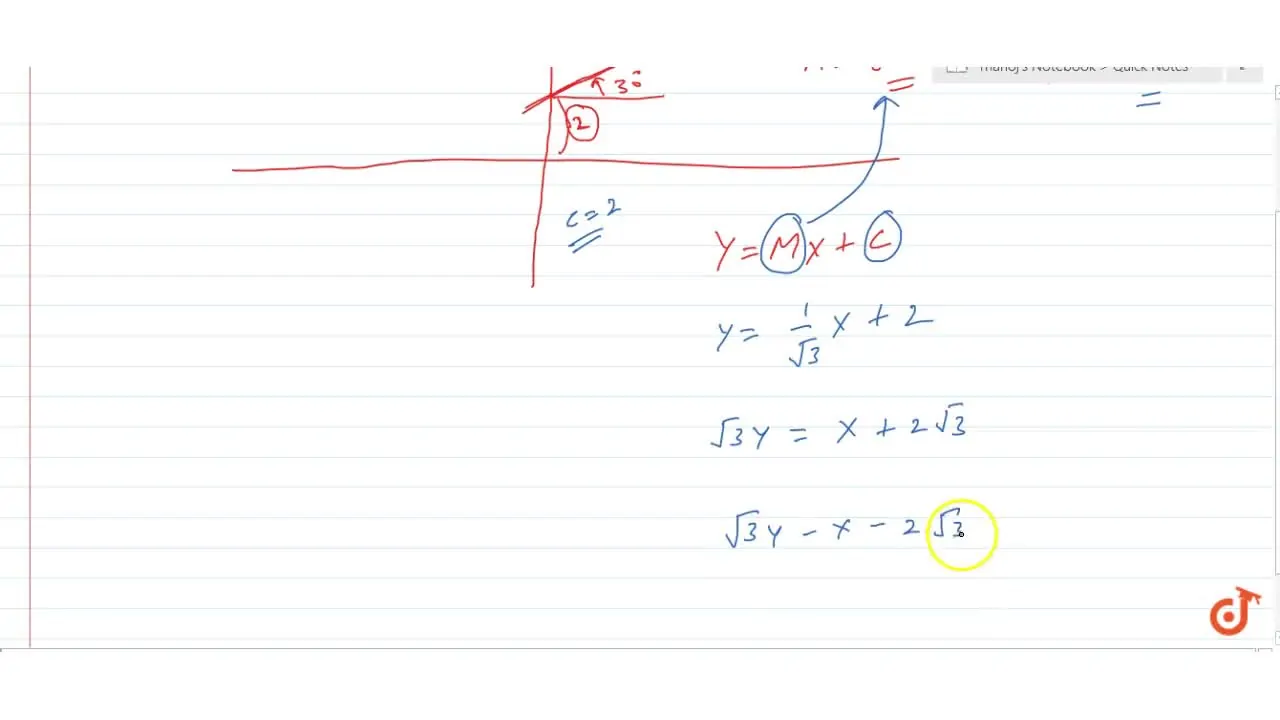
Find the equation of the line which intersects the y-axis at a distance of 2 units above the origin and makes an angle of 300 with the positive direction of the x-axis.
Step by step video & image solution for Find the equation of the line which intersects the y-axis at a distance of 2 units above the origin and makes an angle of 30^0 with the positive direction of the x-axis. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Find the equation of the line which intersects the y-axis at a distance of 2 units above the origin and makes an angle of 300 with the positive direction of the x-axis.
View SolutionFind the equation of the line intersecting the y-axis at a distance 2 units above the origin and making an angle of 300 with the positive direction of x-axis.
View SolutionFind the equation of the straight line interesting y-axis at a distance of 2 units above the origin and making an angle of 00 with the positive direction of the x-axis
View SolutionFind the equation of a line which intersects X-axis at a distance of 2 units on right of origin and makes an angle of 30∘ from positive direction of X-axis.
View SolutionFind the equation of a line which intersects Y-axis at a distance of 4 units above origin and makes an angle of 45∘ from positive direction of X-axis.
View SolutionFind the equation of the line which satisfy the given conditions : Intersecting the yaxis at a distance of 2 units above the origin and making an angle of 30∘with positive direction of the xaxis.
View SolutionFind the equation of a circle which touches y-axis at a distance of 2 units from the origin and cuts an intercept of 3 units with the positive direction of x-axis
View SolutionFind the equation of the line intersecting x-axis at a distance of 3 units to the left of the origin with slope −2.
View SolutionFind the equation of the a circle which touches y-axis at a distance of 4 units from the origin and cuts an intercept of 6 units along the positive direction of x-axis.
View SolutionFind the equation of a circle which touches y-axis at a distance of 4units from the origin and cuts an intercept of 6units along the positive direction of x-a xis
View Solution