Let L1=0andL2=0 be two fixed lines. A variable line is drawn through the origin to cut the two lines at R and S.P. is a point on the line AB such that (m+n)OP=mOR+nOS. Show that the locus of P is a straight line passing through the point of intersection of the given lines R,S,R are on the same side of O).
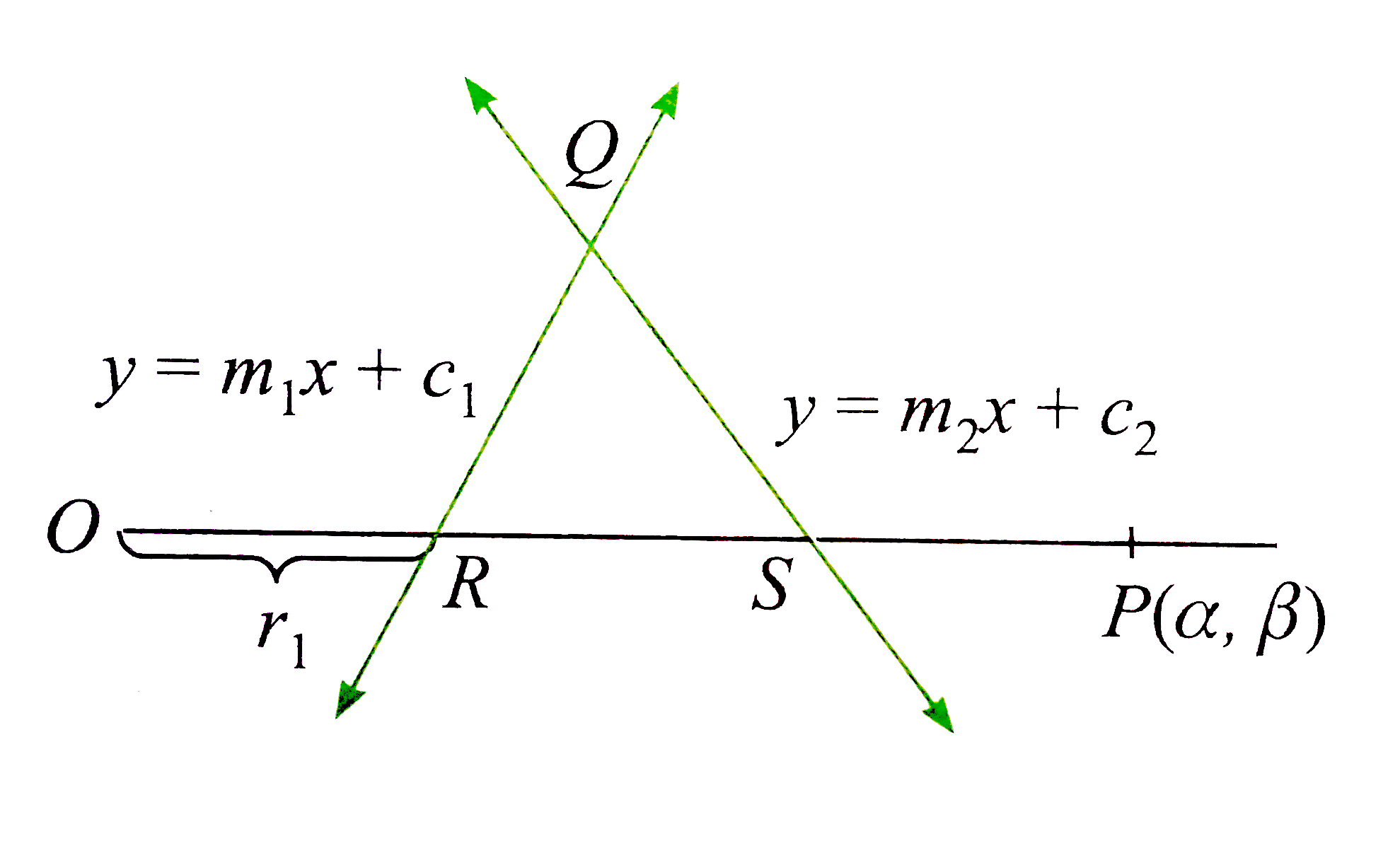
Let the variable line through O makes an angle θ with the positive direction of the x-axis. Any point on this variable line is (O+rcosθ,0+rsinθ)
i.e.,(rcosθ,rsinθ)
Let the fixed lines be
y=m1x+c1 (1)
and y=m2x+c2 (2)
Let OR=r1,OS=r2,OP=r3. So, according to the equation,
m+nr3=mr1+mr2 (3)
Since R and S lie on lines (1) and (2), respectively, we have
r1sinθ=m1(r1cosθ)+c1 (4)
and r2sinθ=m2(r2cosθ)+c2 (5)
LetP≡(α,β). Then,
α=r3cosθ,β=r3sinθ (6)
From (3), (4), and (5), we have
m+nr3=msinθ−m1cosθc1=+nsinθ−m2cosθc2 ltrgt or m+n=mc1(β−m1α)+nc2(β−m2α) [From(6)]
Hence, the locus of P is
m+n=(mc1+nc2)y−(mm1c1+nm2c2)x
or y−m1x−c1+nmc1c2(y−m2x−c2)=0 (7)
Clearly, the locus of P is a straight line passing through the point of intersection of the given lines (1) and (2).
Similar Questions
A variable line is drawn through O to cut two fixed straight lines L1 and L2 in R and S. A point P is chosen the variable line such m+nOP=mOR+nOS Find the locus of P which is a straight ine passing through the point of intersection of L1andL2
View SolutionA straight line is drawn from a fixed point O meeting a fixed straight line in P. A point Q is taken on the line OP such that OP.OQ is constant. Show that the locus of Q is a circle.
View Solution
Knowledge Check
A variable line is drawn through the origin O. Two points A and B same side of O are taken on the line such that OA=1 and OB=2 unit. . Through points A and B two lines are drawn making equal angle α with the line AB. Then the locus of the point of intersection of the lines, is:
Ax2+y2=9+tan2α4Bx2+y2=9−tan2α4Cx2+y2=9+tan2α2Dx2+y2=9+2tan2α4The locus of the centre of the circle passing through the origin O and the points of intersection A and B of any line through (a, b) and the coordinate axes is
Axa+yb=1Bax+by=1Cxa+yb=2Dax+by=2A circle passes through the origin O and cuts the axes at A (a,0) and B (0,b). The image of origin O in the line AB is the point
A(2ab2a2+b2,2a2ba2+b2)B(2a2ba2+b2,2ab2a2+b2)C(2aba2+b2,2aba2+b2)D(a,b)
A straight line passes through a fixed point (2, 3). Locus of the foot of the perpendicular on it drawn from the origin is
View SolutionThrough a given point O a straigt line is drwan to cut two given straight line in R and S. find the locus of a point P on this variable stright line which is such that 2OP=OR+OS
View SolutionA variable straight line passes through a fixed point (h,k). Find the locus of the foot of the perpendicular on it drawn from the origin.
View SolutionA variable line through the point P(2,1) meets the axes at AandB . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionA variable line passes through the fixed point (α,β). The locus of the foot of the perpendicular from the origin on the line is
View Solution
