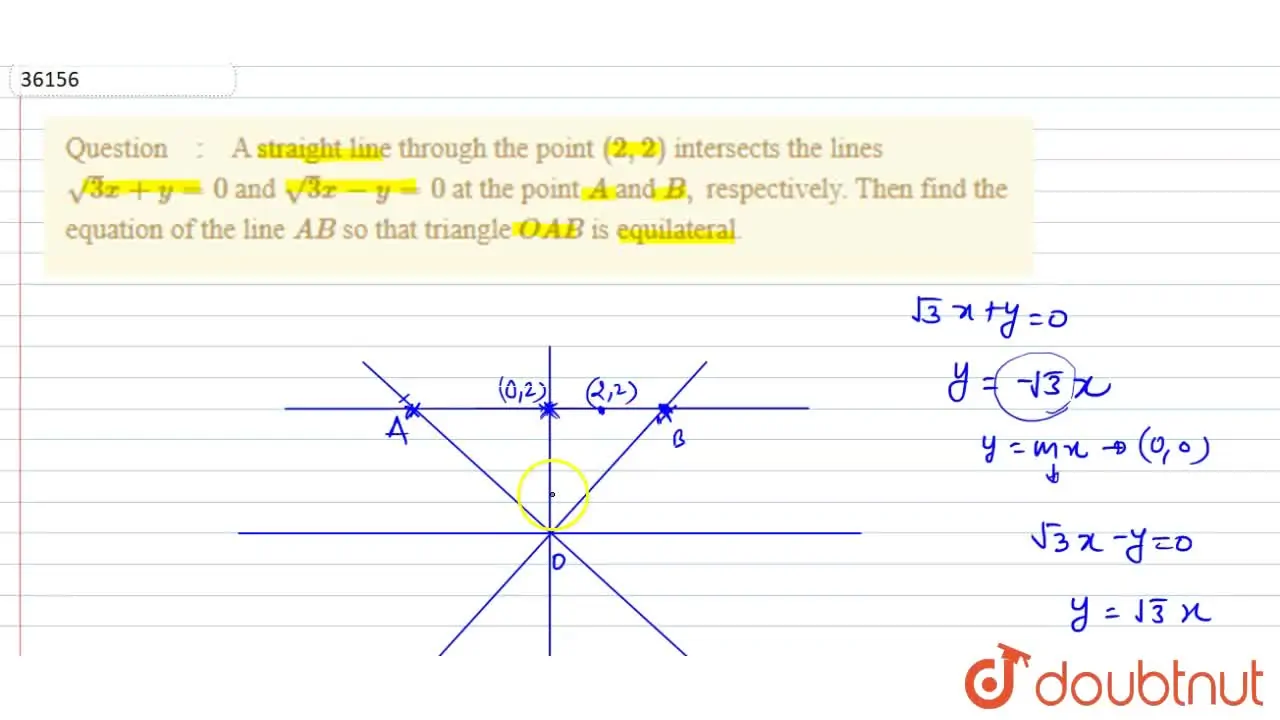
A straight line through the point $(2, 2)$ intersects the lines $\sqrt{3} x + y = 0$ and $\sqrt{3} x - y = 0$ at the point $A$ and $B,$ respectively. Then find the equation of the line $A B$ so that triangle $O A B$ is equilateral.

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the equation of the line $A B$ such that triangle $O A B$ is equilateral, we will follow these steps:
Step 1: Identify the given lines
The given lines are:
1. $\sqrt{3} x + y = 0$ (Line 1)
2. $\sqrt{3} x - y = 0$ (Line 2)
Step 2: Find the slopes of the given lines
Rearranging the equations into slope-intercept form $y = m x + b$ :
- For Line 1:
$y = - \sqrt{3} x$
The slope $m_{1} = - \sqrt{3}$ .
- For Line 2:
$y = \sqrt{3} x$
The slope $m_{2} = \sqrt{3}$ .
Step 3: Determine the angles of the lines
The angles these lines make with the x-axis can be calculated using the tangent of the slopes:
- For Line 1:
$θ_{1} = {tan}^{- 1} (- \sqrt{3}) = - 60^{\circ}$

- For Line 2:
$θ_{2} = {tan}^{- 1} (\sqrt{3}) = 60^{\circ}$
Step 4: Find the coordinates of points A and B
Let the line through point $(2, 2)$ be represented as $y - 2 = m (x - 2)$ .
To find points $A$ and $B$ :
1. Substitute $y = - \sqrt{3} x$ into the line equation:
$- \sqrt{3} x - 2 = m (x - 2)$
Solve for $x$ to find point $A$ .
2. Substitute $y = \sqrt{3} x$ into the line equation:
$\sqrt{3} x - 2 = m (x - 2)$
Solve for $x$ to find point $B$ .
Step 5: Find the conditions for triangle OAB to be equilateral
For triangle $O A B$ to be equilateral, the distances $O A$ , $O B$ , and $A B$ must be equal.
Step 6: Use the distance formula
Using the distance formula:
- Distance $O A = \sqrt{(x_{A} - 0)^{2} + (y_{A} - 0)^{2}}$
- Distance $O B = \sqrt{(x_{B} - 0)^{2} + (y_{B} - 0)^{2}}$
- Distance $A B = \sqrt{(x_{B} - x_{A})^{2} + (y_{B} - y_{A})^{2}}$
Step 7: Set the distances equal
Set $O A = O B = A B$ and solve for the slope $m$ .
Step 8: Find the equation of line AB
Once the coordinates of points $A$ and $B$ are determined, use the two-point form of the line equation:
$y - y_{1} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} (x - x_{1})$
where $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ are the coordinates of points $A$ and $B$ .
Final Equation
After performing the calculations, we find that the equation of the line $A B$ is:
$y = 2$

Updated on:7/8/2024

A straight line through the point (2, 2) intersects the lines $\sqrt{3} x + y = 0$ and $\sqrt{3} x - y = 0$ at the points A and B. The equation of the line AB so that $Δ O A B$ is equilateral, is:
A $x - 2 = 0$
B $y - 2 = 0$
C $x + y - 4 = 0$
DNone of these
A straight line through the point (2,2) intersects the line $\sqrt{3} x + y = 0$ and $\sqrt{3} x - y = 0$ at the points A and B respectively. If O be the origin and $Δ O A B$ be equilateral then the equation of the line AB is
A $x + y - 4 = 0$
B $y - 2 = 0$
C $x - 2 = 0$
DNone
A straight line through the point (2,2) intersects the lines $\sqrt{3} x + y = 0$ and $\sqrt{3} x - y = 0$ at the line AB, so that $△ O A B$ is equilateral, is
Ax-2=0
By-2=0
Cx+y-4=0
DNone of these