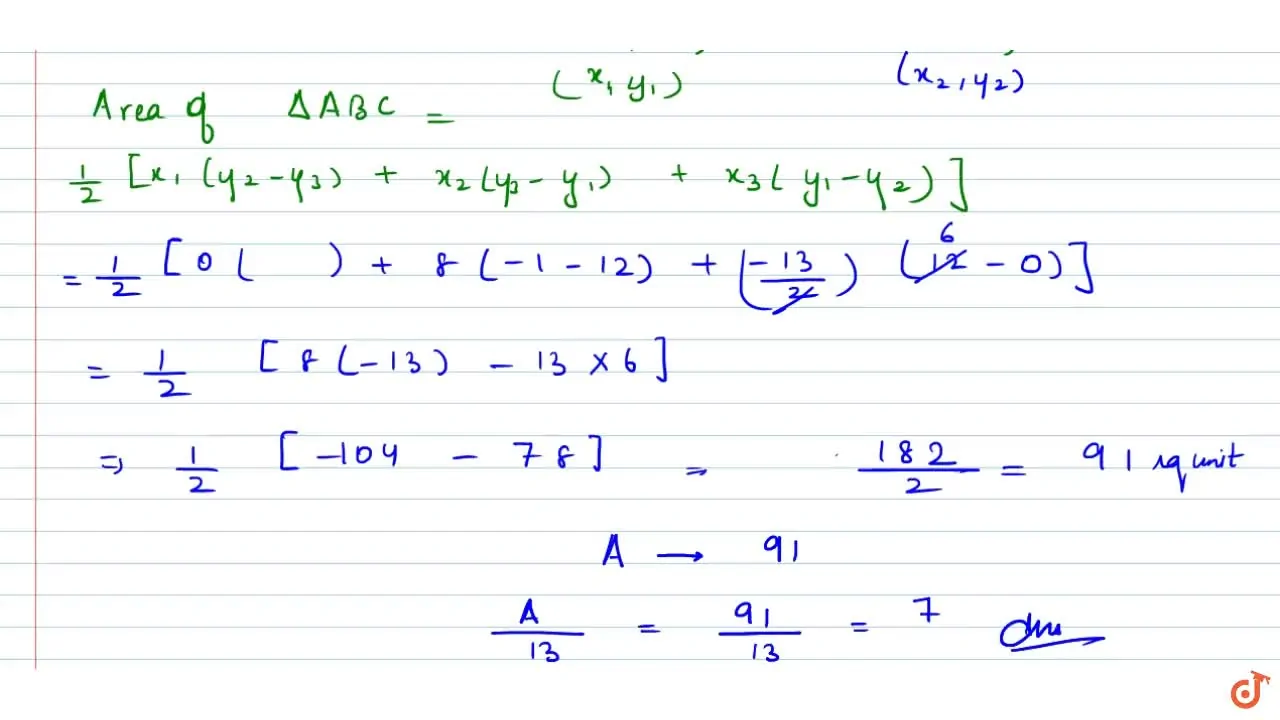The line 3x+2y=24 meets the y-axis at A and the x-axis at B. The perpendicular bisector of AB meets the line through (0,−1) parallel to the x-axis at C. If the area of triangle ABC is A , then the value of A13 is________
Step by step video & image solution for The line 3x+2y=24 meets the y-axis at A and the x-axis at Bdot The perpendicular bisector of A B meets the line through (0,-1) parallel to the x-axis at Cdot If the area of triangle A B C is A , then the value of A/(13) is________ by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
The line 3x+2y=24 meets the y-axis at A and the x-axis at B. The perpendicular bisector of AB meets the line through (0,−1) parallel to the x-axis at C. If the area of triangle ABC is A , then the value of A13 is________
View SolutionThe line 3x+2y=24 meets x - axis at B and the y -axis at A. The perpendicular bisector of AB meets the line through (0, -1) parallel to x -axis at C, then the area of the triangle ABC is_____
View SolutionLine 3x + 2y =24 meets x-axis at A and y- axis at B and perpending bisector of AB meets the line passing through (0,1) and parallel to x-axis at C. Area of ΔABC is
View SolutionThe line 3x−2y=24 meets x-axis at A and y-axis at B. The perpendicular bisector of AB meets the line through (0,−1) and parallel to x-axis at C. Then C is: (A) (−72,−1) (B) (−152,−1) (C) (−112,−1) (D) (−132,−1)
View SolutionStatement -1 : The line 3x + 2y = 24 meets the coordinates axes at A and B , and the perpendicular bisector of AB meets the line through (0,-1) parallel to the x-axis at C . The area of Δ ABC is 91 square units .
Statement-2 : Area of the triangle with vertices at (a,0) , (0,b) and (a , b) is ab/2 sq. units .View SolutionThe line 3x+4y−24=0 cuts the x -axis at A and y-axis at B. Then the increntre of a triangle OAB, where O is the origin is
View SolutionThe line 3x+4y−24=0 cuts the x -axis at A and y-axis at B. Then the increntre of a triangle OAB, where O is the origin is
View Solution" The line "4x+3y=-12" meets x-axis at the point "
View SolutionThe line l in Fig14.14 meets X-axis at A(-5,0) and Y-axis at B(0,-3).
View SolutionFind the equation of the line through (2,3) which is (i) parallel to the x-axis and (ii) parallel to the y-axis.
View Solution